The beginnings of these design studies

These studies began a long time ago and derived from an interest I have always had in mathematics in general, and geometry in particular. Recently I came across a couple of studies that were among the first I carried out; some others have been lost and some are in private ownership. The studies which follow are all based on patterns I saw and explored, and I thought it might be useful to place them here for the record. Unfortunately there is no record of the examples they were taken from, so they will just have to stand as drafting exercises. I should also admit that these sketches are based on the original photographs of the studies, most of the original drawings having been lost – the photographs being the only record I have of them, but which are in too poor condition to be reproduced. A little way below is a more recent examination of the underlying structure.

The illustration above, from which the three following details have been taken, is of one of the original drawings I made in the early 1970s. The width shown is around 280mm of the original. Although the paper has discoloured slightly with the passage of time, the draftsmanship can still be examined. It is placed here to show something of the concentration that goes into study of this character of geometry as well as the accuracy I tried to maintain in drafting. Nowadays, drawing with computer programmes, there are still inaccuracies, but they are easier to deal with than when drawing with ink on paper.

At this degree of magnification it is possible to see how the grain of the paper, a smooth cartridge, interacts with the ink from the drafting pen. It is probable that the two pens used here were 0.2mm and 0.5mm Rapidographs, but I’m not absolutely sure after the passing of over thirty years. You can see there is some blotting at the beginning of lines – look at the red lines top right – as well as a little unevenness in line thickness. I believe I never went over any lines twice as that had a considerable effect on the outcome. In the central junction the red lines have created a star effect. Note that it is not as symmetrical as I would have liked. This might have been due to the lines not drying before a new line was added.

Finally, this detail of one of the junctions illustrates one of the problems of joining lines at bends in the pattern. The pens have a circular nib and have to be held approximately vertically. Where there is a change of direction of the line it is difficult to create a sharp corner. Sometimes this happens, as can be seen on the 120° angle on the left but, on the other two angles this has not been accomplished. Considerable patience was needed in creating these drawings.

It was around fifty years that the first illustration shown above was drawn manually with a Rapidograph pen on a sheet of ordinary paper. Here, for comparison, is the setting out constructed with a computer drafting programme.

The reason for placing the study here after such a long time is that it is noticable that the geometry of the setting out is not as rational as most of the studies which are illustrated later on these pages. Looking at the way in which the lines were placed, particularly with relationship to simple geometry, it can be seen that there is no real logic to many of the connecting points other than that they are located arbitrarily at the intersections of some of the lines. The pattern above is not unattractive, but it does not really represent the simple beauty of the more logical geometric patterns. Perhaps the pattern should be looked at more from the character of its draftsmanship.

This second exercise did not have any construction lines associated with it, as can be seen here. It was carried out to explore the relationship between stars based on ten-point geometry and there must have been construction lines before this was drawn, perhaps just pencilled in as these were all drawn manually rather than with a computer. I have a vague memory that the origin of the pattern was on an Egyptian patterned door, but it is a fairly common pattern and might have come from a number of sources.

This next exercise was carried out in order to explore the construction of a pattern I had noticed as having been drawn with a single, continuous line. The setting out is easily established, being based on four point geometry, the diagonal lines are all base on joining intersections with themselves and with the horizontal and vertical centering lines. It’s a clever construction but one that would have been easy to set out. This type of design is not uncommon, a variety of continuous lines being easily drawn and being suited to a design that interweaves. See the sketch three below.

There are a number of patterns used to produce interlocking tiles, and this is just one of them. Again the basis of the design is four-point geometry set out from the centering horizontal and vertical lines and then just repeated as far as is required. The underlying pattern does not have to be drawn in as much detail as I have shown, but there was something contemplative about this type of drawing that encouraged me to produce similar over-complex constructions, and that can be seen in many of the sketches on these pages.

This is the last of the sketch studies I recorded and was drawn, again, to establish the construction of the pattern on an Egyptian door. Its head is on the left. As you can see, it is another design based on four-point geometry, but the difference here is that the lines that intersect are not as you might expect them to be, but often meet outside obvious junctions. Why this should be so is difficult to say, but it is only when you take the trouble to make investigations such as this that you are able to learn something of the workings of the minds of the original designers.

These two sketechs have been added as although they do not belong to the original drawings, I wanted to see how easily the sketch illustration, three above, could be worked up into – in the first instance – a relatively complex interweaving pattern. I have added a drop shadow to improve the illusion of depth though this would not, of course, be found on a modelled example. Regrettably the sketch is not as symmetrical as it should be, but it does give an indication of how a basic framework may be readily developed into a solid design with the suggestion of a more complex character in its arrangement. Although there are some advantages to working with a computer, it is unlikely I would have made the same mistake had it been drafted. The second sketch probably doesn’t belong on these pages, but is placed here as a notional fountain design based again on the same pattern. It illustrates how readily adaptable these geometric designs might be.

That is all there is of those early studies but, having had to reconstruct them quickly, it may well spur me to see how one or more of them might be developed as suggested in the sketch immediately above. But this may be some way away as there are still a lot of other notes to write…

go to top of page

Geometric basis of patterns

In the context of the notes on this and the preceding page it should be noted that it was with the defeat of the Ummayad empire based in Damascus and the development of the Abbasid dynasty in Baghdad in 762 that a distinct Islamic form of art is said to have developed. Prior to this, Ummayad buildings such as the Grand Mosque in Damascus, a part of which is shown here, were characterised by the Byzantine style of mosaic work, although geometric designs had been a common feature of ornamental work from the later Roman period. The move from the Byzantine style to one of a more geometric character marked a significant change in applied ornamental designs.

This partial view of a mushrabiyah panel – here rotated clockwise through 90° – was photographed in Isfahan, and illustrates an extreme form of pattern design associated by many with Islamic geometry. The use of twelve-point geometry has established the basis for the pattern which is contained within a running pattern to create a frame. The beauty of this pattern is in its neutrality of form and colour, requiring the eye to meander over it, forming and reforming its basic shapes within its constrained field, yet the pattern being possible of expansion infinitely.

The construction of patterns for the purpose of decoration has been the subject of research and investigation for centuries. While I have witnessed the use of straight edges and string in the setting out of Islamic patterns, in watching craftsmen work it is evident that much is carried in their heads as they set out the details governing the patterns they are creating. Just as with this research, albeit over a much shorter time, the knowledge craftsmen have developed has accumulated over centuries.

Nowadays we have greater resources available to investigate pattern conceptualisation and construction; we also have the capability to examine non-Euclidian geometry and create designs which would not have been possible six hundred years ago, as has been effected in this study which has introduced the possibility of extending the beauty of traditional geometries into a third dimension. It is interesting to speculate on how an understanding of this mathematical approach might have altered the artefacts produced by Islamic craftsman in the past, particularly bearing in mind the use of pattern to cover large planar surfaces, and the manner in which this is said to have aided contemplation.

Illustrating the above principle in a little more detail, here are three spheres each of which has the same eight-point pattern applied to them, but at different scales of detail – as well as slight colour variation to the underlying sphere in order to distinguish them further. The exercise is an interesting one in that it might be extended to any curved surface, three-dimensional object.

go to top of page

The muqarnas– three-dimensional design

However, applying pattern to a three-dimensional flat-surfaced is likely to be a much more challenging exercise due to the need to marry the points of the pattern to lines of change of plane. Traditionally this problem has been resolved by creating patterns which are confined within each plane. The decoration of the muqarnasaat at the entrance to this mosque in Shiraz, Iran, illustrates the problem and its traditional resolution here with the lines marking changes of plane emphasised with turquoise, and patterns confined within them.

When mirror work – or, more accurately, cut glass work – is involved, however, it is far more difficult to make out the way in which the muqarnasaat are formed due to the intrinsic character of mirrors. This is particularly noticeable in this first example, seen in a ceiling of the Shah e Cheragh Mausoleum in Shiraz, Iran. While the junctions of of adjacent mirrors create narrow black lines, the reflective character of the mirrors creates far more complex patterns and constructions which flow and change with the movement of the viewer, an interesting experience, one which is enhanced by the lack of colour in the mirrors. In the second example, also photographed in Isfahan, the forms are also set out within a strong geometric framework but the ceiling appears to have less more of an art nouveaufeeling to it and is more easily understood. The work is said to have been carried out in the early eighteenth century, following a fire.

The muqarnas is one of the most recognisable features of Islamic architecture and its underlying three-dimensional geometry. In essence the muqarnas is a form of pendentive, squinch or corbel, the former two being devices to fill the corner of a square structure in order to support a circular or octagonal form above it, and the latter being a device for enabling construction to project beyond the face of a wall or column. The muqarnas can be thought of as a device which fills a zone of transition between one plan form and another on top of it. While the perspective view of this type of arrangement can seem extremely complex – as witnessed in some of the photographs above – the plan form of it is relatively simple. These two photographs are of the same arch in Isfahan, the first looking straight up, the second being a view from outside looking into it, this muqarnas being a relatively simple design.

Here are two more porches, both from Isfahan, and slightly more complicated than those shown above and illustrating a little of the different characters that can be brought to these porches.

The origins of the muqarnas can be traced back to the turn of the 10th century in north-east Iran together with north Africa where it appears to have developed coevally. The first examples of this feature have been argued as being essentially decorative, being carved in plaster on the interior of domestic buildings, though it appears that the muqarnas began to develop as a structural device around the same time as a method of enabling square plan forms to hold different geometrical shapes above them. This enabled internal spaces to develop spatial characters that were impossible utilising beam structures. Domed spaces were one type of volume benefitting from the use of muqarnasaat, as were porches, or iwaanaat as can be seen in these two photographs.

But whereas these muqarnasaat were designed to allow spaces to be covered in a highly decorative manner, a possibly earlier development might have been the use of muqarnasaat to corbel out from a column or burj in order to establish capitals on columns, balconies around manaaraat and so on. This would have resolved both a structural as well as a decorative function and would have been simpler to effect and develop.

These two photographs, both taken in Isfahan, Iran, show an example of each. The first is of the capital of a wooden column, one of forty holding up the roof of the Chehel Sotoun, from which the building takes its name. The enlarging of the head of the column would have served a structural function in providing a greater base on which to set beams supporting the roof. As is evident from this photograph, it also fulfils a classic visual function in providing a transition point for the eye.

The second photograph is of the head of the Sareban manara, constructed in the Seljuk period, around 1140 AD. The photograph, taken in 1975, shows the head of the tower in some state of decay which I believe has now been repaired. The muqarnasaat clearly demonstrate how it was possible to corbel out a structure from the shaft of the burj in order to provide support for the shurfa or balcony from which the faithful would have been called to prayer.

The point of all these examples is to illustrate how structural and decorative devices were based on coherent geometrical rules, creating beauty from structural necessity in a manner developed from two-dimensional geometries.

more to be written…

go to top of page

A little more on the use of mirrors

A little has been written above about the use of mirrors in Islamic designs, but mainly in relation to their use on pendentives or strong three-dimensional forms. As suggested, the work above as well as here to the side, has not been carried out in mirrors but in cut glass, the term ‘mirror’ being used as descriptive shorthand. You can compare the effect to some extent with this modern work by Monir Farmanfarmaian exhibited at the Victorian and Albert Museum, London, in 2011.

These three photographs were taken in 1975 at the Mausoleum of Mir Sayyed Ahmad, the son of the seventh Imam in Shiraz, Iran – the Shah-e-Cheragh and the third most important shrine in Iran. They illustrate something of the richness that cut glass can bring to interiors compared with coloured tiles, plasterwork or timberwork. Part of this beauty derives from the mobile quality and colour of the light reflected from its facetted faces.

But the first photograph, above, also illustrates something of the distraction brought about by the use of the glass, the reflections and slight eccentricities of the construction both enriching and dissipating the accuracy latent in the geometric substructure. Compared with the structural articulation of, say, Western religious buildings, this treatment creates a more contemplative feeling in its diffusing effect.

This second photograph is of a part of a wall surface and shows the rich effect of the cut glass set in a geometric pattern, the two panels being constructed on the basis of ten-point geometry. Even though the flat wall surface is an easier surface on which to apply the cut glass accurately, the small variations both in cutting and setting the elements of the pattern can be seen to bring an enlivening richness to the pattern, the light catching the glass at slightly different angles.

This third photograph is a detail of a different part of the wall, but showing better how the plane of the wall has been enlivened by the facetted design. I have not been able to discover when the decorative wall treatment was carried out. Construction of the building was begun in the twelfth century but work of addition, replacement and repair has been carried out well into the twentieth century, particularly due to earthquake damage. Whenever this work was made it is evident that considerable skill has gone into the cutting and assembling of the pieces to enliven the walls and ceilings.

go to top of page

A basis for variety

This first illustration is of one of the simplest ways to begin looking at patterns and their constructions. The basic shape created is that of an octagon, and inspection of the lines shows something of the possibilities that might be accomplished using this as a basis for a pattern.

From the centre of a horizontal blue line a vertical line is constructed and, from their intersection, diagonal lines are drawn at 45°. At the common intersection of the four lines a red circle has been drawn.

With their centres at the intersection of the blue lines with the red circle, eight orange circles have been described, each with the same diameter as the red circle. Note that the intersection of each pair of orange circles coincides with a horiontal, vertical or diagonal blue line.

At the intersection of the blue lines and the orange circles intersection a purple octagon can be drawn, and that at the outer intersection of each orange circle and the blue lines, a larger purple octagon can be drawn. Green lines have been added showing more common intersections. It is evident that additional lines can be drawn to create a more complex basis for pattern making.

The graphic illustration below shows a basis for creating patterns which are derived from the turning of elements around a central point, creating a regular number of equally sized shapes. From this the patterns are developed generally through the connection of intersecting points. In contrast, this animated illustration demonstrates how the simple selection of points can affect the pattern. The two partial patterns are both based on twelve point geometry. The only difference between them is the selection of the inner point at which the lines meet; this affects the apparent density of the panel through the relative visual densities of the central rosette with the radiating petals.

On a more prosaic level, execution of design and other work in the Gulf has, as a result of a number of factors, been relatively simple and has generally derived from the simple patterns based on four, five and six point geometries. I have never seen designs based on seven, nine or more complex geometries in Qatar. Although geometric patterns are found in nature it is likely that they would not have been observed by designers in the Gulf as there is little of this nature to see; rather they would have developed from the simple tools needed to create the pattern geometries. However, there is the likely relationship of designers working coevally on the other side of the Gulf, and it is true that many craftsmen worked on both sides of the Gulf, some of them moving up to Qatar from Dubai, across the Gulf from Iran, as well as from the Indian sub-continent. If this is so, then they seem to have brought little of any complexity with them. One reason may have been the lack of glazing capability on the west side of the Gulf in those days, and the lack of funds with which to import them from Iran. Geometric patterns on the Arabian peninsula were essentially limited to timber and, particularly, naqsh work.

Compare that tradition with this example, a detail of the curved underside of the roof of the monument to the Persian poet, Khwaaja Shams al-Din Muhammad Haafez Shiraazi, known as Hafez, in Shiraz, Iran, which has been established upon a sixteen point geometry. I believe the work was carried out in 1931 under the direction of André Godard, at that time director of the Archeological Services of Iran, with Maxime Siroux, and was based on their extensive understanding of the Safavid architecture of the region. The open kiosk appears to be around four or five metres in diameter, copper roofed and resting on eight columns enlivened with muqarnas capitals. Although the photograph appears to be slightly distorted, the pattern seems to be regular in its geometry and relaxing in its effect.

At first glance the work appears to be another fine example of Islamic tilework, the main rosette creating a powerful image that would be enhanced by its being viewed in a position where the structure has been elevated a metre from its approach at ground level by five surrounding steps. Predominately yellow-based tilework sets the base colour of the pattern within which darker tiles create the petal effect within the pattern.

Yet, like many Islamic patterned works, there is considerable variety in the setting out of tiles and colours, an effect which creates vibrancy in what is otherwise a discrete example of a pattern which might be extended infinitely – despite the fact that the pattern occupies the internal face of a domed structure.

It is a commonplace in many designed pieces that variety is created by eccentricities in the work. This can be for a number of reasons which would include, but might not be limited to the result of direction by the master craftsman, mistakes by the artisans, irregularities in the manufactured or cut tiles, the setting out, the ground on which the work is attached, or a combination of any or all of these. But there is another reason given to me which might also apply here. It is said that only Allah is perfect and that, if a work strives for perfection, then there is a dangerous intent demonstrated by the artisan. This is a reason given both for irrationalities in carpets as well as in work of this nature.

There are a number of interesting areas to look at in the pattern, but for the purposes of this note on setting out, there are two which stand out. The first one is the layout of one of the sixteen dark petals, that which sits at around five-thirty in the above photograph and is shown in detail in the centre here. The petals each contain two double pairs of blue kite-shaped tiles which sit, more or less, at right angles to each other. This detail shows that this one petal has the two pairs in parallel, a very obvious departure from the setting out of the other petals and, most likely, a deliberate amendment to the design by the master craftsman rather than a mistake.

But the most obvious departure from a perfectly established geometric framework is that seen at the centre of the design. Here, as shown in this detail, the predominately yellow tilework surrounding the central opening is essentially based on a regular square grid. It must be anticipated there would be a ready geometrical or notional connection to the surrounding sixteen-point star. Yet there is not. The grid appears to be oriented to the diameter of the central circle in one direction – here approximately at 45° top right to bottom left – but there is no corresponding alignment at right angles as might have been expected. Nor is there any happy coincidence where the yellow pattern meets the angles of the sixteen-point star. Again, it is such an obvious design decision that it can only be understood as a deliberate decision, one which creates for me a visual frisson at the heart of the design.

It may be that the above design is relatively simplistic in concept and execution, and that the eccentricities are more evident because of it, so it is instructive to compare that pattern with a more complex example, this one being the internal dome of the Sheikh Lotf Allah mosque, Isfahan. The mosque was constructed between 1603 and 1618, so the work considerably pre-dates the tomb of Hafez by over three hundred years and, more important in the context of this note, illustrates something of the beauty and complexity of the Safavid work of that period. More particularly, although the pattern is based on sixteen-point geometry, the intricate foliate decoration, allied with close colour tones, creates a much more sophisticated design, the underlying geometry being discernible only on close examination, an exercise likely to enhance the experience of those using the mosque.

These next two designs are details of the ceiling of the Masjed-e Shah in Isfahan, one of the masterpieces of Safavid architecture and constructed between 1611 and 1629, the period partly coincident with the Sheikh Lotf Allah mosque above. The setting out, again, is based on sixteen or thirty-two point geometry, a choice which seems to be common to many of these dome designs. The seven-coloured polychrome tiles were, apparently, an invention necessitated by the intention to carry out the project quickly. Despite the work being carried out by extremely skilful artisans, critics believe it to be inferior to the tilework of the Sheikh Lotf Allah mosque.

The wider colour variation in the tiles appears to create a more easily readable pattern, compared with the work in the Sheikh Lotf Allah mosque. Here the different design elements establish lineal patterns radiating from the centre. The gold tiles in the centre of the design are, by contrast, far more complex than the centre of the Sheikh Lotf Allah design, seeming intent on concentrating the viewer’s eye at the centre of the design, rather than encouraging it to roam across the wider design. I am not absolutely sure, but I believe there are recessed elements in this central part of the design which, if it is true, may be related to cutouts used in the music room of the Ali Qapu palace, dating from around the same time. The cutouts there were used, it is said, as cupboards, though it seems unlikely for those illustrated here at the higher levels of the design which was executed in relatively fragile plasterwork. Compare the work of these pendentives with those above.

The design of the ceiling of the tomb of Hafez illustrates a easily comprehensible geometric pattern compared with the two Isfahan ceilings below it. Here is another Isfahan ceiling which illustrates another readily understood design, again based on sixteen-point geometry but using blue vase-shaped elements radiating from the centre alternating with calligraphic panels, the latter perhaps the work of the famous calligrapher, Reza Abbasi, who was working on the Masjed-e Shah at that time.

The beginning of this note, above, introduced a simple way in which connecting points in twelve-point geometry might be selected in order to produce relatively small differences in a particular rosette pattern. The issue of selection is especially important to understand when looking at the design of rosettes. The craftsman or designer working up a pattern has a significant number of choices available within the circumscribing circle in order to maintain a systematic selection from naturally related points of connection. This illustration shows one such series of alternatives, this time relating to a ten-point rosette. The selection of internal angles of the different petals have been restricted to intersecting lines falling along the radiating red lines. Other design decisions are, of course, possible.

The basic construction of the ten-pointed rosette is not shown here but can be found elsewhere on this page. At its simplest it can be seen that all lines connecting the twenty points on the circumference of the circle have been joined, creating a matrix of intersections within the circle.

The rosettes here are mostly convergent, in that the lines forming their petals converge towards the containing circle. However the first two are divergent and the third, parallel. This characteristic is a feature in the different geometries for such rosettes – five-point, six-point and so on – and needs to be considered when establishing patterns outside the containing circles in order to produce rational linkage with the infinite repetitions characteristic of Islamic designs. The last two steps in this graphic are not, of course, rosettes, but have been added to carry through the logic of joining the available points of intersection, and produce respectively a decagon and icosagon.

A little more has been written about the linking of ten-point rosettes further down the page.

The next part of these notes was researched and written in the 1990s. Since then I have discovered that a treatise – Kitab fi ma yahtaj ilayh al-sani min al-amal al handasiyya – was written by Abu al-Wafa (940-998) in Baghdad on the use of the straight edge and compass by artisans. It had been thought that it was an instruction manual for artisans but is now thought more likely to be a description of their work for intellectuals.

go to top of page

The beginnings of Arabic mathematics

For centuries, mathematics was more advanced in the Arab world than in the Christian West, and was treated not only as an intellectual exercise, but also as a functional system for organising a number of practical operations. The times of prayer, the division of inheritances and the direction of the qibla were such operations, but mathematics was also closely related to astronomy and astrology, the times and dates associated with the religious observances requiring a degree of precision. In particular trigonometry, spherical geometry, algebra and arithmetic were involved in determining elements of these observances. The bases on which these disciplines rest have developed differently. Modern mathematics is grounded in a base-ten numeration system; this governs most of our mathematical systems, and has done so for a considerable time. But it has not always been the case.

The mathematics of the Arab world is likely to have developed through Egypt, Greece and India, but originated in Mesopotamia around four thousand years ago. There, the system of numeration was sexagesimal, or rooted on base-sixty, a figure which we continue to use today with hours, minutes and seconds of time, and degrees, minutes and seconds in geometry and astronomy. In Britain, it was only in 1971 that decimal currency supplanted the system where one pound Sterling comprised twenty shillings, each of twelve pence, thus making 240 pence to the pound. This was a system introduced by the Romans to Anglo-Saxon Britain when their silver pound was divided into 240 pennies.

There are many advantages to a sexagesimal system as the number 60 is a composite number being capable of division by 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60 – compared with the decimal system where the number 10 is only divisible by 1, 2, 5 and ten, and where there is no capability for dividing by 3. However, this was not a pure system as the writing of the numbers – in fact their formation as cuneiform symbols impressed into clay tablets – was executed to the sub-base of 10, there being only ten symbols used to represent the individual numbers, not sixty.

The form of numbers was similar to that we use nowadays in that the larger valued place numbers were ranged from the left. This contrasted with the later Egyptian, Greek and Roman systems. However, it has to be borne in mind that the concept of zero had yet to be conceived – it was introduced from India around 500 AD – so there has been difficulty in interpreting some numbers accurately. More recently it is claimed that the earliest zero known can be found engraved on a stone in Cambodia, is dated precisely to 683 AD, and that the concept of zero was likely to have been a European invention, not Indian or at least Eastern, as most suggest.

There appears to be no real understanding of why the base-sixty came into being, although it has been suggested that it might be a direct result of a primitive counting system using the thumb to count off the twelve segments of the four fingers of one hand, and combining this with the five fingers of the other hand to produce five multiples of twelve – 60. A simple counting system relying on parts of the body is an attractive theory and makes considerable sense at a time when there were no commonly available recording systems or materials. But it might well have a different origin, of course…

Throughout these notes there are references to differences in meaning between ‘Islamic’ and ‘Arabic’, terms commonly misused or misapplied. In the sense it is used here the term ‘Arabic mathematics’ refers to mathematics developed within the golden age of the Islamic world, that part of the world stretching from India in the east to North Africa and Spain in the West, and between the seventh and seventeenth centuries. It was particularly centred in the region that is now Iraq and Iran. Through this area the common language was Arabic and, while there were a variety of religions, the dominant one was Islam, giving rise to the inaccurate term, ‘Islamic mathematics’.

The conquests and spread of early Islam developed rapidly, bringing change in the areas to which the new religion moved. In conformance with Ibn Khaldun’s theory of the cycle of civilisation, the development of political and cultural institutions took some time to become established, but by the second half of the eighth century progress in both arts and sciences was notable. Much of the initial work on the sciences was the work of Muslims translating Indian, Babylonian and Greek works into Arabic, the former two sources gradually being eclipsed and subsumed by development of the Greek works. Some of this translation was the work of al-Saabi’ Thabit ibn Qurra at the direction of Abu Ja’far al-Maa’muwn, the Abbasid caliph who ruled from Baghdad between 813 and 833.

One of the important concepts in mathematics was introduced from India, that of Hindu, or Arab-Indic numerals, adopted from earlier work by both Arabic and Persian mathematicians in the ninth century and, from them, transferred to Europe in the Middle Ages.

Between the twelfth and seventeeth centuries, European scholars regularly referred to earlier Arabic texts. Leonardo Pisano – more commonly known as Fibonacci – writing in his book ‘Liber Abbaci’ in 1202, noted the work of the Persian, Muhammad Abu Musa al-Khawarizmi, 780-850 AD, and referred to his ‘Al-Kitab al-mukhtasar fi hisab al-jabr wa al muqaabala’, which was translated in 1145 as ‘Liber algebrae et almucabala’, as an important mathematical resource.

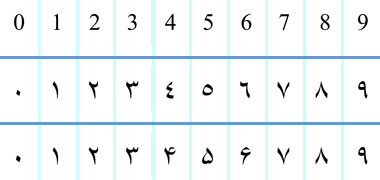
In al-Khawarizmi’s book ‘Algoritmi de numero Indorum’, or ‘The Hindu art of reckoning’, he introduced a more workable series of ten figures – the numerals 0 to 9 – than the system being used in Europe up to that date. It now became possible to describe any number precisely, the ten numerals permitting a more rational approach to calculations. This illustration shows corresponding Arab-Indic numbers along the centre with, below them, Eastern Arab-Indic numbers common to Persian and Urdu.

While there has been some debate as to when the concept of decimals appeared, it seems to be accepted that it was Abu al-Hasan Ahmad ibn Ibrahim al-Uqlidisi who introduced the place value decimal system as early as the tenth century.

This photograph shows a portion of text by al-Uqlidisi showing a dashed oblique mark over the numeral ‘9’ of the number ‘17968’ indicating the position of the decimal point over the ones – in this case, denoting the number 179.68. Note that, in contradistinction to Arabic which is written from right to left, Arabic numerals are written from left to right.

Other areas of mathematics also showed the influence of Arab mathematicians. For instance al-Khwarizmi, used his study on Islamic inheritance law as an impetus behind the formation of algebra, also an area of interest to Abu al-Qasim Muhammad ibn Abdullah al-Hashimi al-Qurashi. And the North African, al-Hassar, working in the twelfth century, was responsible for the modern symbolic mathematical notation for fractions which separates the numerator and denominator by a horizontal line.

It is now commonly understood that many English words are derived from Arabic; ‘algebra’, ‘algorithm’, ‘sine’ and ‘zero’ are words commonly used in the area of mathematics, but there are many more in the fields of astronomy and medicine, all illustrating the debt there is to scientists writing in Arabic.

more to be written…

go to top of page

Arabic geometry

The first Arabic writings on geometry can be dated from the early ninth century with the publication of Muhammd ibn Musa al Khwaarizmi’s treatise on algebra in which there is a considerable section dealing with geometry in his chapter on measurement – bab al misaaha. Following this publication there was a extensive body of work produced in Arabic, much of it dependent upon Greek and other earlier writings, but increasingly incorporating original thinking. They might be loosely divided into three general categories:

• translations of Greek and other languages as well as original work derived from them. The main source was Euclid’s ‘Elements’, but works by Archimedes, Apollonius, Theodosius and Menelaus were also referred to,
• geometric contributions to other sciences, particularly astronomy, and
• manuals for those working in the field of surveying and building construction.

Considerable advances were made by Arabs in sciences generally, and in medicine, astronomy and mathematics more specifically. Apart from medical instruments, perhaps one of the most familiar objects to us are the attractive designs of the alustrlaab or astrolabe, used both to make astrological and astronomical observations, surveying, and the marking of prayer times as well as in way-finding. It was also used for astrological purposes both in the Islamic world and, later, in Europe. A form of astrolabe was developed for use in navigating at sea to take account of the movement of the sea.

Much of Khwaarizmi’s work – who died around 850 – was based on Greek writings, but it is interesting to note that other sources were the Chinese astronomer, Chang Heng, (78 to 139), and the Indian astronomer, Brahmagupta (born 598), both of whom had calculated the value of pi, their methods and results being slightly different from Khwaarizmi, but an advance from the work of Archimedes.

The concept of pi, or π, has fascinated mathematicians for centuries. An irrational number, it is the number that is the ratio of the diameter of a circle to its circumference – c = πd – where ‘c’ is the circumference of the circle, and ‘d’ its diameter. Its beauty can be thought to lie in the fact that it is an irrational number that has no pattern of numbers within it, yet this random sequence relates directly to the simple perfection of a circle.

It also has connections with other areas of mathematics, such as in connecting numbers theory with geometry. For instance π can be shown to relate to a sequence of odd numbers – π is equal to the sum of four times the sum of one, minus a third plus a fifth minus a seventh plus a ninth …

π = 4 ( 1 – ⅓ + ⅕ – … )

However, the important point to bear in mind with respect to π in this aside, is its connection to cyclical calculations.

Later, Abu al-Wafaa noted a number of geometric rules that would have assisted artisans in their work and, following him, al-Karaji wrote similarly on geometric constructions in his al-kaafi fi ’ilm al-hisaab – The Sufficient in the Science of Arithmetic. The importance of these works, and others that came later, is that an interface between algebra and geometry was established. He is considered to have been the first writer to free algebra from the constraints of geometry, itself an outcome of preceding Greek mathematical work.

In the middle of the ninth century, kitaab ma’rifa misaahat al-ashkaal al-basita wa al-kuriyya – The Book of the Knowledge of Measuring Plane and Spherical Figures – was published, the work of three brothers, Muhammad, Ahmad and al-Hassan Banu Musa. But it wasn’t until centuries later that Jamshid al-Kaashi, who died in the early fifteenth century, surpassed the accuracy of calculating pi by a method which, while based on Archimedes’ work, used as a basis significantly more polygons inscribed within a circle than Archimedes – 3x2²⁸– 805,306,368, compared with the latter’s 3x2⁵– 96. The work in which this was published was titled al-risaala al-muhitiyya – Treatise on the Circumference. The result turned out to be correct to sixteen decimal places, the same accuracy being attained, one hundred and fifty years later, by the Dutch scientist, van Roomen using, as a basis, inscribed and circumscribed polygons of 2³⁰. It is notable that Arab mathematicians believed pi to be irrational, but it wasn’t until 1766 that Lambert succeeded in proving this to be true. It is held that the interest of Arabic mathematicians in these fields of algebra and geometry was responsible for restoring these areas of science to the heights they had enjoyed in Babylon and, later, Greece and its territories.

While the work described above dealt in considerable accuracy with geometry, both two- and three-dimensional, and its relationship, particularly, with algebra, more practical methods were being developed in order to carry out day-to-day work associated with surveying and the construction of building works.

Today we have an interest in the use of compasses and straight edges to establish shapes, but evidence is that from an early time, a knotted string was the medium for establishing at least a right angle. For instance, divided into twelve equal parts, a knotted string was capable of immediately producing the right angle of a triangle of three, four and five sides, a figure that was held to have magical properties. Note in the diagram that the circle inscribed within the triangle has the same diameter as the circle, with centre ‘C’. It is considered probable that other strings were used to fulfill a range of simple geometric functions associated with the need to survey and set out constructions. Moreover, by this time it is probable that simple compasses and, perhaps, marked rulers, were used in relatively simple works.

The Greeks ascribed the invention of compasses to Thales, who died over two and a half thousand years ago, and much of the work of geometry carried out by the Greeks was based on methods involving compasses as well as rulers with special markings. Archimedes, for instance, used a ruler with two marked points to trisect angles. As I wrote earlier, much of the work of Arab mathematicians is important in that they developed their thinking on the basis of previous Greek and earlier mathematicians and, in the process of transcribing and drawing this opus together – as well as adding to that knowledge – spread their work through the medium of the Arabic language, the lingua franca of Islam.

Much of earlier Greek work has been lost to us and we must be grateful to Arab mathematicians who carried out work based on Greek traditions. For instance, Thaabit ibn Qurra ibn Marwan al-Sabi al-Harrani, a student of the Banu Musa brothers and writing in the ninth century, re-established work of Socrates and Archimedes, from the latter setting out a proof for a heptagon, the original having been lost. Abu Nasr al-Faaraabi and the previously mentioned Abu al-Wafaa both produced books relating to geometrical constructions, with the book by al-Wafaa containing most of the work of al-Faaraabi. This established a number of practical operations such as the setting out of simple constructions with ruler and compasses, in particular, the creation of four, five, six, eight and ten sided figures. But he also showed how an approximation of a seven-sided figure might be constructed and, by using a method for trisecting an angle, a nine-sided figure. In addition he illlustrated how a number of other, more complex, three-dimensional constructions might be effected.

Arab mathematicians continued to move forward the understanding of earlier mathematicians through examination, development and invention. Basic concepts were readdressed and redefined in order to produce a more sound foundation for geometry as well as other areas of mathematics. Issues relating to parallel lines, for instance, were worked on for hundreds of years and formed the basis for later European work. Geometric transformations, projections – an area relating to determining the direction of the qibla – a particular interest of Abu Rayhan Muhammad ibn Ahmad al-Biruni around the turn of the eleventh century, spherical geometry and, from this, latitude, longitude and, of course, the sciences relating to the astrolabe, a device originating in Greece.

In summary Arab mathematicians, in common with Arabs operating in scientific areas, produced work based heavily on Hellenistic principles but, in doing so both preserved and expanded this opus as well as propagating this knowledge widely through the medium of the Arab language and the influence of Islam. This enabled later European mathematicians and scientists to benefit from a significant body of work in developing these disciplines.

go to top of page

Tools used in the design and layout of patterns

In the past traditional designs would be made with simple compasses and a straight edge, the same tools which can be observed in use by designers working in Iran and the Gulf to this day, though with the addition of a device to construct right angles and to develop parallel lines. While I have seen wooden triangular squares and string used in Iran I do not recall seeing T-squares.

Nor am I able to say if the systems used were the same all over the Middle East; but in Egypt the tools used to draw decagons included a T-square and two fixed set squares made in the form of 36° / 54° / 90° and 72° / 18° / 90° triangles. Using the T-square, parallel lines and squares could be constructed and, with the two triangles, ten sided figures could be drawn without the need of a pair of compasses. The triangles and T-square are illustrated here, though not to scale.

This next series of three drawings illustrate how the triangles and set square, notionally illustrated above, were used to set up a framework upon which ten-sided figures would have been established. It is instructive to compare this practical system for constructing decagons with that described below which utilises a pair of compasses and a straight edge.

The first drawing, shown above, illustrates a sequence of four steps utilising a square grid, but rotating and mirroring it twice, then overlaying each in order to create a two-dimensional framework from which a number of design decisions can be made.

To begin the process, establish a grid whose lines are set at the radius of the decagon that is to be created. These radii establish construction lines of the decagon that will be tangents to the circle inscribed within it. For this stage the T-square and one of the right angled triangles would have been used.

The second two sketches of the above drawing show, in blue and red respectively, the same grid rotated by, respectively, 18° and 54° and both reflected and laid on each other. This will have been carried out with the use of the two set triangles. The fourth sketch shows all the grids superimposed on each other. This last sketch is shown in greater detail in the large drawing below it.

The last of these three drawings illustrates how the decagon – shown as the inner red line – has been formed by following lines of the grid. There is also a second decagon – shown by a blue line. Two pentagons – shown in pale blue and red – have also been shown. What is significant, though it is not shown in this sketch, is that a number of different decagons can be outlined based on the grid pattern. This allows for the possibility of significant variations for craftsmen working up patterns. While this encourages variations in the shaping of the decagon – compare the shapes of the blue and red decagons above – additional variations are made by the linking of the basic pattern to other similar or dissimilar patterns.

The extent to which the designs are then developed is apparently a matter for the master mason or individual craftsman, the main factor being the speed with which the work has to be executed, particularly when working in a medium such as juss which dries rapidly. Because of this, carved plaster work is relatively simple in Qatar and approximations rapidly executed in wet plaster. Where the work is made in plaster which is set, more care can be taken.

Within buildings, as well as on their faces, the designs of naqsh panels are always different. Sometimes there is reflection of designs facing each other within a majlis, for instance, but in the main an effort is made to ensure that no two designs within a single space are the same.

go to top of page

A basis for measurement

My observations have been that Arabic craftsmen setting out their designs, whether as running designs or within panels, need to measure in order to be able to obtain point coincidence and accuracy. Tape measures and rulers may be used, but often the old ways are still in operation, or were when I started these notes…

Many of the notes on these pages deal with the construction of shapes, generally moving from the easier to the more complicated, and using the simplest of tools to generate the shapes – sometimes with a fixed-angled device but, most frequently, a straight edge and compasses, the latter often a piece of string used with chalk, charcoal or a nail, essentially anything that will make a legible and removable mark.

Nowadays there are more modern tools available and used, but there is still the need to establish certain elements of a design in order to ensure the materials used fit the space available for the design; and that requires the establishing of relationships.

This pair of diagrams illustrate how simple divisions enabling a range of divisions and sub-divisions can be made without the need of a measuring tool.

The first square, Diagram 1, shows an easy way of dividing a line in order to break it down into a half, quarter, eighth, sixteenth and so on. It requires the ability to be able to construct a square, and a straight edge to mark the dividing lines. A straight edge or even a string can be used to mark or snap the lines.

The second square, Diagram 2, shows the slightly more complicated way in which a line can be broken down to thirds from which a sixth, ninth, twelfth and eighteenth and so on can be established.

The first two diagrams look at the relatively easier divisions to make, the third, Diagram 3, shows how a line can be divided into five equal parts.

Construct a square, draw its diagonals as well as join the centres of opposite sides. Now draw four lines, each connecting the centre of each side to one of the two alterntive opposite corners in a symmetrical manner. These will intersect in four points to create an angled square. Draw vertical lines through each of these intersections to divide the square – and top and bottom lines – into five equal parts.

Finally here, in Diagram 4, there is a method for dividing a line into any number of equal sections, in this case dividing a line into seven equal parts.

From one end of the line – in this case, the left – draw a line at any acute angle and of any length. In this case the line is little longer than the line to be divided. With compasses set at a suitable distance, step off the number of divisions you wish to have on the original line. Draw a line joining the last division made with the end of the original line and then, at the same angle, draw parallel lines back to meet the original line.

go to top of page

Basis for geometry – constructible geometries

While some of the geometrical constructions are not found in Qatar, set out below are the basic methods by which 3, 4, 5, 6, 8 and 10 point patterns can be constructed using only a straight edge and compass, the standard site tools used to set out designs in naqsh. Constructions of 7 and 9 point patterns can be approximated, as can others, but there is rarely a need for them in Qatari naqsh work.

From the geometrical constructions mentioned above generally, patterns with a greater complexity can be constructed. Patterns with 12, 15, 16 and 20 are readily established though approximations of 14 and 18 can be made based on approximate constructions for 7 and 9. I don’t know how to construct 13 and 19 point patterns, though there is a construction for 17. However, I digress… The next few notes look at the construction of these more complicated shapes.

Shapes that are capable of being constructed with an unmarked straight edge and compasses are known as constructible polygons and begin with polygons with sides that are: 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96, 102, 120, 128, 136, 160, 170, 192, 204, 240, 255, 256, 257, 272, 320, 340, 384, 408, 480, 510, 512, 514, 544, 640, 680, 768, 771, 816, 960, 1020, 1024, 1028, 1088, 1280, 1285…

Shapes that are not capable of being constructed with an unmarked straight edge and compasses begin with polygons with sides that are: 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 31, 33, 35, 36, 37, 38, 39, 41, 42, 43, 44, 45, 46, 47, 49, 50, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 65, 66, 67, 69, 70, 71, 72, 73, 74, 75…

go to top of page

Three point geometry

Three point geometry can be constructed from six point geometry, it should be noted that it is not possible to subdivide an angle into three parts in Euclidean geometry. However, there is a construction that permits an angle being divided equally into three using only a straight edge and compass; that is by fitting the angle to a previously constructed construction. This is illustrated elsewhere on this page.

go to top of page

Four point geometry

Four point geometry is one of the easiest geometries to set out. It is often used in counterpoint with circular geometries. At its simplest, it is constructed by raising a perpendicular from the centre point of a horizontal line to the point where it cuts a circle described from that point, and joining the four points of intersection. The circle is established with its diameter being set at the length of the required diagonal of the square. Further sub-divisions into eight point geometry can be constructed by sub-dividing the sides of the square.

The construction of the square above is only one of a number of ways of constructing a square. Should it be necessary to have it organised along a horizontal line rather than at 45°, then that is not much more difficult, the following method being one of them. The description is longer than the actual construction…

Draw a horizontal line. With the radius of a pair of compasses set to the length of the side of the required square, describe a circle centred on the horizontal line.

From the two points where the circle intersects with the horizontal line draw arcs above and below the horizontal line and join the points of their intersection. This establishes the left vertical side of the square. From the point of intersection of the circle and horizontal line draw a second circle of the same diameter.

From the point of intersection of this circle and the horizontal line, repeat the foregoing to create the line that will establish the second vertical side of the square. From the centre of the first circle to the intersection of the second circle and vertical lines draw a line which will establish the diagonal of the square at 45° from the centre of the circle. Complete the square.

There are a number of different ways of looking at the construction of squares. Here is a simplified version of another of them.

First, draw a horizontal line and, at its centre, describe a circle. At the two points where the circle intersects with the line, draw two circles with the same diameter as the first. These two circles will touch each other tangentially at the centre of the first circle.

Although the details for drawing its construction have not been shown here, raise a vertical line at the centre of the first circle. This will intersect with the first circle twice. Joining these two intersections will create the vertical line. At the two points of intersection of the vertical line with the central circle draw two circles with the same diameter as the first circle.

The outer four circles will mutually intersect and, joining those points of intersection, a square will be created.

If the points of intersection of the horizontal and vertical lines with the first circle are joined, a smaller square on the diagonal will be created, its area exactly half that of the larger square and its diagonal, of course, the length of the side of the square.

As illustrated in the animation on the right, this characteristic of the geometry can be repeated with the squares becoming increasingly small, the pattern being found in a number of traditional designs.

On the left is an illustration of two additional squares which can be constructed within the main square by using the natural points of intersection of the circles and the first rotated square.

There are many designs which use squares, the simplest being those having a checkerboard effect and with, at the least, two alternative colours for contrast. This simple animation illustrates a few of the many ways in which a pattern can be created. There is more relating to the disposition of shapes to form patterns elsewhere. But these six patterns are just used as an introduction to the geometries that can be derived from the simple square, particularly when it is turned at an angle. This next exercise has a regular grid as its basis, against which squares have been rotated and repeated.

Even though the organisation of these geometries has a four point basis, the patterns formed can have a strong dynamic character to them created solely through the rotation of one of the pattern elements. In this case the first pattern has been created with two shapes – rows and columns of alternating squares and lozenges. Due to the manner in which we view patterns such as this, there is a liveliness caused not only by the two-dimensional motion of the elements, but also a three-dimensional character created by our association of representational forms in two-dimensions. The eye wants to understand that the pattern represents a collection of cubes or stacked blocks, yet the pattern does not do that; it is solely a two-dimensional treatment.

The second graphic above illustrates the construction, the pattern being created by joining corners of the blue squares to create the basic angled squares and lozenges. It is a very simple pattern. Note that the red squares are moved along by four units of the blue squares as is shown in this third illustration.

If the red squares are moved along by only three units of the blue squares, this pattern will emerge, one that apparently introduces a third shape, a smaller angled white square, into the pattern. In fact, the smaller white squares represent the second line of squares in the first diagram and, if the logic is to be retained, should be not white but beige, the same colour as the main squares.

To illustrate how this simple mechanism – of moving the squares incrementally – this fifth graphic illustrates how the pattern would turn out if the squares are moved along by five units of the blue squared grid. Here, again, the logical colouring would be to have the white squares the same colour as the original squares, beige. But, like the illustration above, they have been left white to give definition to the exercise.

go to top of page

√2 geometry

Related to this is the development of geometries based on the diagonal of a square – √2 where the side is 1 unit. The geometries of the Alhambra depend, to some extent, on this geometry rather than on the Golden Section – 1:1.414 compared with 1:1.618. I don’t know why this should be so, though there is the Greco-Roman tradition, as mentioned above in the note on cosmatesque designs, of the use of √2 geometries in two dimensional patterning.

The second diagram illustrates the difference between the basic two proportions. Note that the √2 proportions are those of the International ‘A’ paper sizes – A4, the most commonly used, being 210mm x 297mm.

Here are illustrations of the paper standards adopted by the International Organisation for Standardisation from the German standard which has been in use there for over eighty years and has now been adopted in most of the world except the United States and Canada. The ‘A’ series, on the right, is based on a sheet of paper having a total area of one square metre and its sides, as mentioned above, in the proportion of 1:1.414. Each time the paper is halved the proportions of the new sheet remain the same. The ‘B’ series, on the left, is mainly used for posters and in the book industry and has sides in the same proportion, but with the sides of the basic sheet being 1.000 x 1.414 metres.

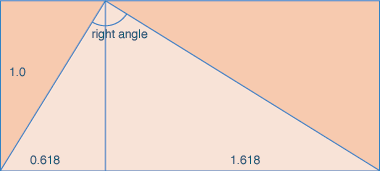
Incidentally, the area relationship between a square of side one unit, and a rectangle of sides 1.618 to 0.618 – the golden section, is the same – 1. There is an interesting note to be read here on some of the characteristics of φ – phi – the 21st letter of the Greek alphabet, and which is used to represent the golden number, mean or section.

It has been said that the use of this geometry and the the complexity of the elements of design in this development, led to the intricacy and intellectual complexity of the Alhambra. This geometry is also used in the Gulf, but there isn’t the complexity of arrangement and interplay of proportions in these simpler buildings, the relationships being found only in two-dimensional patterns.

The issue of proportions introduced by this note on √2 geometry, is a subject I want to come back to later. It relates not just to the Golden Section mentioned below, nor to classical architecture, but also to the search for perfect proportions that has been continuing for centuries.

Although this may not be the most obvious place to introduce this mathematical curiosity, here is an illustration of a right angled triangle with sides in the proportion of 3:4:5, the latter being the diameter of the circle. It can be found within a hexahedron – or rectangular cuboid – by joining the internal diagonal corners of the shape which has sides in the proportions of length 4 and square ends of √4.5 or 2.121. There would be a similar construction for a 5:12:13 right angled triangle, the square end being √12.5.

go to top of page

√3 geometry

While √2 appears in the construction of many geometric designs so, too, does √3. The development of a rectangle with its sides in the proportion of √3:1 is relatively easy, being related to six point geometry and the extensive appearance of angles of 60° – dropping a vertical from the apex of an equilateral triangle with its internal angles of 60° and with sides of 2 units, will create a vertical of √3.

To construct such a rectangle, describe a circle and, with the compasses set at the same radius and with one point on the circumference, describe a second circle which will cut the first in two places. Extending a line from each of those points of intersection through the centre of the two circles to cut the circles in a second place will create two points which, when joined, will create an equilateral triangle with internal angles of 60°.

Repeat this to construct a second triangle and then draw two lines each tangent to the inner sides of the two circles to intersect with the bases of the two equilateral triangles. Joining those points will create a rectangle whose sides are in the proportion √3:1.

go to top of page

√5 geometry

Coincidentally, the same or similar construction will produce another rectangle which contains a diagonal of √5 length. In this case, the two sides of the rectangle are produced to intersect with the circumferences of the two circles, in effect creating a rectangle of two squares sharing their bases on the central, horizontal line. Obviously, with the sides of the extended rectangle being 1 unit and 2 units respectively, the diagonal must be √5.

go to top of page

Triangle and octagon approximations

One of the benefits of being able to construct geometries readily, is the ability to keep within tolerable limits of accuracy with relatively simple tools. Much of the work on these pages relates to the search for geometries that can be constructed with a compass and straight edge. But certain constructions became possible and suggested dimensions that, in turn, became generators for setting out. In effect, these measurements decided both shapes and proportions.

Such a system was employed by the Mughals who used the relationship between the numbers 7, 12, 17 and 24 to set out developments. There are three points to remember:

• An octagon whose width – not radius – is 17, will have a side with a length of 7,
• a right angled triangle with a side length of 12 will have a hypotenuse length of 17, and
• a right angled triangle with a side length of 17 will have a hypotenuse length of 24.

But if you take a closer look at the geometry involved you will see that these are very much approximations.

This first illustration shows the dimensions as described above. The red triangle has right-angled sides of 17 and a hypotenuse of 24, the blue triangle right-angled sides of 12 and a hypotenuse of 17, while the black octagon has sides of 7 and a width of 17. The geometry fits together accurately enough at this scale, so it is understandable that those using it must have been reasonably sure that it was accurate enough for their purposes.

Examining the diagrams in a little more detail, this second illustration reveals the mathematics behind the approximations. If you look at the two triangles of right-angled sides 5 and 7, with their respective hypotenuses of 7 and 10, you will understand that there is a small discrepancy in each of them.

These are drawn as 5² + 5² = 7² or 49, and 7² + 7² = 10² or 100.

But mathematically these should be 5² + 5² = √50, or 7.07106781², and 7² + 7² = √98 or 9.89949494² respectively. This is an error of just over 0.1% – one centimetre in ten metres – perhaps not that significant when setting out buildings in those days.

go to top of page

Five point geometry

Five point geometries are slightly more difficult to construct, but can be relatively easily developed. They have an additional interest in that they are similar in proportion to the geometry derived from the Golden Section, having proportions between the minor and major chords of the five points circumscribed by a circle, of 1:1.618. From the five point geometry, ten point geometries are easily developed and form the basis for many of the more attractive patterns in Islamic decoration. They are not that common in the Gulf due, perhaps, to the difficulties associated with their construction.

There are many construction methods for basic five and ten point geometries; one of the simpler ones is illustrated here.

Begin with a line which is to form one of the faces of a five-sided figure. With a centre established at each end of the line, describe two circles whose radius is the length of the line. These two circles will intersect with each other twice. Draw a line between these two points. In this case it’s the vertical line.

With a centre based on the lower of the two points of intersection and with a radius established from that point to the ends of the original line, draw an arc which will intersect with the first two circles twice each.

Draw lines from the lower intersections of the new circle and the first two circles, extending them through the intersection of the third circle and the vertical line. These lines will intersect with the first two circles.

Draw lines from the ends of the first line to these two points of intersection and you will have created the next two sides of the pentagon. To obtain the final point necessary to complete the five sides, draw two arcs, their centres based on the previous points of intersection of lines and circles. Complete the five sides of the pentagon.

One of the interesting natural characteristics of the pentagon is shown in this illustration. The internal isosceles triangle, shown in pale blue, has its lower two angles each twice that of the top angle – respectively 72° and 36°. The isosceles triangle, shown in lilac, has its top angle three times that of its lower two angles – respectively 108° and 36°, the internal angles of the pentagon being equally trisected.

go to top of page

A pattern developed from a golden triangle

The diagram immediately above illustrates, in light blue, what has been termed a ‘golden triangle’, the isosceles triangle whose base is set in a golden ratio to the length of the two long sides – φ=(1+√5)/2 – the angle at the top of the triangle being 36°, the two on the base, each 72°.

This feature has been used in the construction of a grid framing a traditional dodecagonal star polygon design. The benefit of this method of construction is that it can be readily constructed with straight edge and compasses. Although it may seem a little complicated it might be worth explaining the process alongside the following animation. More and better detail can be found in this paper from which this animation is derived.

In order to simplify the adjacent animation, the first stage of the construction – the creation of the rectangular frame – has been created with the base of the triangle horizontal. The construction that follows has the rectangular frame turned for illustrative purposes so that its short side is horizontal.

Begin by constructing a regular pentagon as is illustrated in the diagram two diagrams above. The construction of the pentagon uses five equally sized circles, and they form the elements that establish the proportions of the panel, the sides of the inscribed golden triangle within the pentagon forming one side and one diagonal of the panel. The construction of the other two sides of the panel are not shown here but should be readily understood and capable of construction by raising lines at right angles to the first two sides of the rectangle from the points of their intersection with the circles.

Now, draw the diagonals of the panel and establish a point half way between the bottom left hand corner and the crossing of the two diagonals and draw a line at right angles through it. Bisect the angle between the diagonal and the left hand side of the panel and, from its intersection with the right-angled line, bisect the angle between it and the previous bisector.

Draw a circle with its centre on the bottom left hand corner and its radius set to the point of intersection of the diagonal and second bisector. Draw a smaller circle with its centre at the point from which the second bisector was drawn, and its radius set to the point of intersection for the previous, larger circle.

Inside the smaller circle it is possible to draw a small pentagon and, utilising previous construction lines, two more small pentagons can be established, mutually touching, their bases lying along the circumference of the larger circle. Again, I have not shown all the construction lines in order to maintain a degree of simplicity.

This pattern of pentagons can be transferred to the four corners of the panel and lines added linking them. Next, a secondary grid is drawn through the centre points of the pentagons. Using the grid as a guide, a central ten-pointed star can be drawn together with additional lines completing the pattern within the panel. This panel is capable of being used to create an infinite ground of ten-pointed stars.

The above two sketches illustrate something of the power of the basic design when assembled in small and large groupings.

As mentioned above, there are a number of ways in which a pentagon can be constructed using only a pair of compasses and a straight edge. Here is another method illustrating how a pentagon may be constructed within a circle.

Draw a horizontal line and at its centre describe a circle. From this centre, develop a vertical line – in this graphic, the construction is not shown. Using points at the centre of the circle and its intersection with the horizontal line, construct a vertical line that bisects the horizontal line between the centre of the circle and its intersection with the circle.

From the point of intersection between this second vertical line and the horizontal line, and with a radius of half that distance, draw a circle. Now, from the point of intersection of the first vertical line with the bottom of the large circle, extend a line which joins the intersection of the horizontal and second vertical lines, projecting it to intersect with the small circle.

With its centre on the intersection of the vertical line and large circle, and radius set to the intersection of the small circle with the last drawn line, draw an arc to cut the first circle in two places. These will locate two of the corners of the pentagon. With centres on these two points and the same radius, draw arcs that will cut the outer circle at the top centre and at the bottom in two places. These locate the other three points of the pentagon.

go to top of page

Pentagons and some of their characteristics

The perimeter of a regular pentagon delineates the most efficient way in which its area can be enclosed. Certain special forms of a pentagon, such as Cairo and Prismatic pentagons, have a slightly longer perimeter – less than a unit square, which is 4 but, at 2√(2+√3) ≈ 3·86, is more than ≈ 3·81 for a regular pentagon. The first sketch to the right demonstrates the difference between these two shapes, illustrating each of them circumscribed around a equally sized circle for a direct comparison.

The second of these two sketches illustrates how a plane might be continuously tiled by a combination of the Cairo and Prismatic tile, this pattern being only one of a number of alternative ways in which the combination might be effected.

As discussed above, regular pentagons have an intrinsic beauty to them, incorporating as they do approximations with the Golden Section. But an interesting quality of pentagons is that, in common with triangles, squares and hexagons, they can be tiled on a plane – albeit not using regular equilateral pentagons which require an additional shape to enable this. One of these pentagons is the Cairo pentagon, which can be tiled on a plane either by itself or in conjunction with Prismatic tiles – a tile which includes three joined sides of equal length and set at right angles to each other. This is illustrated in the sketch above. There are many other forms of convex pentagons which also respect the capability of tiling a plane. While there only five possible arrangements of equilateral pentagons that may be tiled on a plane, there are – or were until you read the note below – fourteen known arrangements for tiling convex pentagons on a plane, and which are illustrated here.

Some time ago I made a note, immediately above, stating that there were only fourteen ways in which an irregular pentagon could be used to tile a plane. While the documentation of tiling relating to three, four and six sided shapes is thought to be complete, five-sided shapes have proved to be more evasive in terms of discovering the ability of variations that might tile a plane.

More work has been carried out on this mathematical puzzle and a fifteenth has now been found. Not only this, but its discoverer believes there may be more than this waiting to be added to the fifteen as it has not been mathematically proved that there can only be this number. The fifteenth is illustrated to the side at a similar scale to those previously found.

This graphic illustrates the shape of the tile that forms the basis for the continuous tiling of a plane. Sides AE, ED and BC are each half the length of side AB. Angle AED is a right angle and, with the other four internal angles of A – 105°, B – 150°, C – 60° and D – 135°, together make up 540°, the sum of the internal angles of a pentagon.

The compound graphic here illustrates some of the characteristics of the fifteenth tiling pattern capable of covering a plane.

You should be able to see that the basic tile is reflected and rotated in order to provide a complete cover to the plane.

The graphic is intended to show something of the complexity of the pattern by first showing the pattern with only a single coloured tile. This is the same pattern as is illustrated in the lower yellow illustration a little way above.

The second version here shows how the pattern is developed through the use of three colours. These correspond to the differentiations used to illustrate it in an article announcing its discovery.

The third version identifies the two handed versions of the tile and illustrates how the two versions interlock.

The fourth and fifth versions show the six individual orientations of the different left and right handed tiles.

The purple tile has orientations that rotate through 0°, 90°, 150°, 180°, 270° and 330°, while the red tile has orientations that rotate through 30°, 60°, 150°, 210°, 240° and 330°. For comparison, the orientation of the tiles in this illustration are the same as those in the graphic above.

go to top of page

A development of five point geometry – the Cairo pentagon

This first illustration appears to be a simple design based on a deformed regular pentagon. It is of a pattern based on what is commonly known as a Cairo pentagon due to the belief that it was extensively used in that city. Although there have been a number of references to this tiling, it has been commonly thought that there appears to be no evidence of its use other than in diagrammatic forms such as this. However, in mid-November 2010, evidence of its use in pavements has surfaced and is published elsewhere. Below, I have added some photographs of the tiles, courtesy of Helen Donnelly, to illustrate this character of geometry.

On first viewing, the tile on which the pattern is based, appears to have been formed by squashing or distorting a regular pentagon. In fact this is not the case. Instead, the geometry is based on a 45° setting out and, while the top four sides are of equal length, the base is slightly longer. This creates a shape where the internal angle measured at the base is 112.5° compared with the 108° of all the angles of a regular pentagon. The construction is not difficult, though perhaps it may seem so from my over-developed illustration here.

On a horizontal base that will form the bottom side of the pentagon, raise two vertical lines and, from the right angles formed between these and the base line, construct two lines at 45° angles bisecting the right angles. These two bisecting lines will meet the verticals, creating a square with sides the length of the base.

Now bisect the 45° angles between the two verticals and the 45° bisectors, creating two more angles of 22.5° each. The apex of the pentagon tile will be located at the point where these two bisectors meet. Join the apex and one end of the base side, locate its central point and construct a line perpendicular to it. From the apex, draw a line that passes through the corner of the square previously defined and extend it to intersect with the previous line drawn as the perpendicular. That point is the location of the upper corner of the pentagon. Repeat this construction for the other side. Note the difference in length between the base side and the other four sides in the different radii of the blue and red circles.

The construction is relatively simple, certainly compared with that above. From the centre of a horizontal base that forms one side of the pentagon, raise a vertical line. From their central junction extend two diagonal lines at 45° bisecting the right angle formed between the base line and vertical line. With compasses set at the distance between the two ends of the base line and the centre at one end, describe a circle that cuts the diagonal line. Repeat for the other side. With the compasses set at the same distance and centred on these two points of intersection, draw arcs that will bisect at their meeting with the vertical line. This construction, based on Martin Gardner’s work in the Scientific American magazine, gives internal angles between the base line and adjacent sides of 114° 18’ and a top angle of 131° 24’.

These next two sketches illustrate the equal-sided pentagon tile used in a congruent tiling pattern, together with the underlying geometry. In many cases, as this note started, Cairo tiles appear to have a long base compared with the other four sides, but here the equally-sided pentagon can be seen to have its relationship in Archimedian geometry. More on this can be learned from an article published in Mathematics Magazine. In the lower sketch the Archimedian geometry can be seen in the blue lines, delineating an arrangement of isosceles triangles and squares. Were the pentagons to be regular, than the geometry would be comprised of equilateral rather than isosceles triangles. As a regular pattern this can be seen to be extendable indefinitely and is the basis for the Cairo tile pattern which has been quoted for years, but for which no photographic evidence has been found – until November 2010.

The illustrations given above have been constructed on the basis of specifically sized squares and kite shapes underlying the tiles. But there are other ways of constructing a similar tile. Here you can see that an underlying grid has Cairo tile shapes formed by simply joining up intersections of the grid. Notice that the tiles formed have a more squashed shape compared with those immediately above, but it might be seen to be a swift way of producing these characteristic pentagons. This and the sketch below, both illustrate alternative ways of drawing the same pentagon.

It has been pointed out to me that there is an easier construction, both for a pentagon with sides of equal length, as well as one whose base is of a different length to the other four sides, as in this example. The beauty of this particular construction is that it is simple to create the tiles with a pair of compasses set at a single diameter, and a straight edge. All that is required is for a horizontal line to be drawn upon which a series of circles are constructed half a diameter apart. This is then repeated vertically. The only lines not shown here in the basic construction are those that should be used to create the vertical from the horizontal starting line. On the left is a grid similar to that above.

These next photographs were taken of pedestrian paving areas in a part of Cairo that seems to have been missed by those who have previously written about what are known as ‘Cairo tiles’. The tiles come in two types: square and lozenge.

The first two photographs appear to me to be of two different prefabricated tiles suggesting that there was more than one contract to provide and lay tiles in this area. This might be a result either of the area to be covered being large or, more likely, the timing of the contracts – one more recent than the other. The first photograph is likely to be the older tile, the significant difficulty with it being its inaccurate setting out when seen in its context as being an element of congruent tiling. Most evident at the top left of the photograph, the tile has been fabricated with the whole width of the recessed pattern line at its left and right edges. In order to tile accurately this should have taken account of the joint between the tiles. By contrast, the second photograph illustrates what appears a more accurate design to the prefabricated tile, the combined width of the recessed line on two adjacent tiles now being the same as those lines within the rest of the tiles.

Here is a detail of what I believe to be the older prefabricated tiling, the difference between the recessed detail at its edge being clearly wider than that within the rest of the tile. Working from photographs is not easy so it is not possible to analyse the tile with too much accuracy, but my guess is that it is a square tile, and that the pattern can not be geometrically accurate in order to take this width into account. What is significant is that the tiles are prefabricated as square tiles and not as lozenges as might have been an alternative, with each lozenge formed by four pentagons. When accuracy in laying tiles is certain, rectangular tiles are easy to lay. Lozenge shaped tiles take up inaccuracies readily, but will require more cutting and fitting when coming against straight lines.

What is significant is that the tiles are prefabricated as square tiles and not as lozenges as might have been an alternative, with each lozenge formed by four pentagons. When accuracy in laying tiles is certain, rectangular tiles are easy to lay. Lozenge shaped tiles take up inaccuracies readily, but will require more cutting and fitting when joining straight lines.

The other notable feature is that the tiles are obviously not based on an equal-sided pentagon, the base side being significantly longer than the other four sides. As stated previously, the planes of the pattern do not take proper account of the junction of adjacent tiles. It is difficult to work out exactly how these tiles are designed, but this sketch illustrates a possible way of setting out the tiles which might have appealed to a contractor. It produces an approximation of the pentagons, with those lying with their axis vertically being slightly different from those lying with their axis horizontal.

Unlike the tiles shown in the photographs above, these two sketches are made with equal-sided pentagons. They illustrate how the setting out should have been made in order to establish, on a square tile, the recessed groove widths that would give congruent tiles the correct pattern widths where the tiles meet. Any groove lying along the edge of the square would need to be half the width of those grooves in the rest of the tile. In fact they should also take account of any gap between the tiles, there normally being an allowance in laying for variation of two or three millimetres depending on the tolerance of manufacture of the tiles. From a practical point of view, as suggested in the previous paragraph, it is possible to take a number of liberties with the setting out in order to produce what might appear to be Cairo pentagons. The small red sketch on the photograph in the paragraph above illustrates one type of approach. This would produce pentagons, but those lying along the horizontal axis will be slightly different from those along the vertical axis – though to the casual observer they will appear similar, if not the same. In these two examples, all pentagons – together with their defining lines – are equal in shape and size.

But the tiling illustrated above is not the only type that makes use of the pentagon for its shape. Here are two more photographs, taken in Cairo, of Cairo pentagon tilings, this time taking the form of individual pentagons. The first photograph shows an individual tile that has been lifted away from the pavement. Its broken top corner gives the impression that the tile is made up from mosaic pieces, but this is unlikely due to the need to mass-produce paving. The tiles are much more probably precast as are the square tiles shown above.

The tiles have been produced in four colourways, thus giving the opportunity to vary paving patterns and produce more varied designs over the area in which the paving is deployed. Red and yellow colouring are very common in this form of concrete tile, black less so though, as can be seen in this photograph, it introduces a useful contrast. Bear in mind that Cairo is a particularly dusty city, a factor that helps to bring out the pattern of the grooves.

But the obvious difficulty with tiles that are not orthogonal is in the accuracy of their junction with linear walls, kerbs and roads. This requires concrete cutting saws and labour, both additional expenses to a contractor, as well as leading to inaccuracies in site work when compared with the controls that can be applied to off-site pre-cast work. Where large contracts can be planned and junctions considered, then it might be possible to produce a range of tiles that will make up the spaces between pentagons and linear runs. In work of the nature shown, this is unlikely to have been the case, and evidence is that make-up and replacement has been made with smaller, orthogonal tiles or bricks. Regrettably, pavements are notoriously prone to damage by successive contractors working on the utility structures commonly laid below them. Make-up work is usually poor and, in this case, it suggests that the pentagonal tiles were in place before the orthogonal tiles.

This sketch is based on the photograph located two photographs above. Although it is not as accurate as I would like, I believe it will serve its purpose. The group of four pentagons that form a lozenge in the original photograph have been isolated and distorted in order to form a regular figure. The purpose is to illustrate the probable geometry behind the shape of the lozenge and its component pentagons – the sketch now being more easily comparable with the two geometrical drawings shown above this group of photographs.

This, again, is a distorted image of a part of the photograph above. The purpose is to give an indication of the internal detail of the tile within the construction of a – more or less – accurate tile. It is not possible to work out how or why the pattern might be as it is but it is evidently made up of four, five, six and seven sided figures, symmetrically located about a vertical axis drawn through the central, top point of the pentagon. What makes this pattern interesting is that it follows a tradition of Arabic geometrical designs that have logical constructions behind them; here this appears not to be the case and I wonder how the construction was derived. Note that the shapes making up the pattern have only a notional relationship with the shapes on adjoining tiles.

Coincidentally, a door has been discovered, also in Cairo, which has been constructed with a version of the geometric design characteristic of the Cairo tiles. It appears to be of relatively recent manufacture, perhaps no more than twenty or thirty years. Notice that the pentagonal design used to create the pattern on the panels of the door is different from the pattern used on the doors’ adjacenet panels. The latter appear similar but are obviously based on six point geometry.

But the most obvious difference between the setting out of these pentagons and those of the pavement tiles illustrated above is that the base of the pentagons on the wooden panel are shorter than the lengths of other four sides. You should also be able to see that the basic pattern of the panel detailing has similarities to a common pattern – found both in the Islamic world and elseswhere – the axehead or hammerhead pattern, that is illustrated on the previous page.

If you compare the geometry used to set out the axehead design with that behind these pentagonal designs, you will see that the circles establishing the former design are set further apart than those here due to the junctions of the circles being coincident. As in many patterns of this nature, the simple lines encourage the viewer to follow them, moving the eye from lineal to areal elements of the pattern, the setting out of the lines being more sophisticated than appears to be the case at first sight.

Note the similarity in the photographs above – illustrating the pavement tiles and door panelling – of the geometrical shape of the pentagons. They appear to share the characteristics not only of being pentagons, but also of having two pairs of sides set at right angles to each other. The only different element appears to be the length of the base line which is longer in the case of the pavement tile than is the length of the wooden door panelling.

The construction of a pentagon that is related to the Golden Section is given below where the sides and internal angles of the pentagon are equal, creating internal angles each of 108°, the sum of the internal angles of a pentagon being 540°.

But the characteristic of the Cairo tile patterns shown above are that they have a base and four equal sides, these latter consisting of two pairs meeting at right angles. This diagram illustrates the construction of a pentagon that has its four sides of equal length above a base of shorter length, the two pairs of sides having junctions at right angles. The top angle and the two associated with the base are all equal and of 120°. The construction is simple and would be easy to construct using just a straight edge and pair of compasses.

To begin with, draw a horizontal straight line that will form the base. With the radius of a compass set at this length, draw two circles that will intersect above and below the base. Raise a vertical line through the centre point of the base.

From the point of intersection of the two circles above the base, draw a third circle of the same diameter as the first two. The point at which this circle and the vertical line meet will be the corner of the top corner of the pentagon.

Project lines from the ends of the base line through the two outer intersections of the three circles. These lines will be established with internal angles of 120° to the base line.

Describe a fourth, smaller circle from the same centre as the third circle, its radius being established by the distance of the centre point to the base line which will form a tangent to that circle.

From the top point of the pentagon, draw two tangents to this circle that will each intersect one of the lines projected at 120° from the base. These will form the two outer corners of the pentagon and will each be a right angle.

As mentioned previously, the internal angles of this pentagon are two at right angles and three of 120° each, from which it can be seen that the ratio of each of the four equal sides of the pentagon to the base will be 1:√3-1.

The pentagon incorporates triangles – shown here in grey – that contain a right angle and two angles each of 60° and 30°. These will have their sides in the proportion of √3:1/2 where 1 is the length of its hypotenuse – here the notional length given to four sides of the pentagon. Subtracting one of the non-hypotenuse sides from the other gives √3-1/2, which is half the length of the base which must, therefore, be √3-1 in length.

It is evident that the pentagon that is created with four of its sides arranged as pairs set at right angles to each other may form a number of pentagons, varying only with the length of the base side. Theoretically they will vary from a rectangle – shown on the left of this illustration – to a square, the latter set at 45° as shown on the right. The pentagon discussed above is shown in grey as one of the possible constructions of this range of setting out for a pentagon. The arrows indicating the movement are also in grey.

The above illustration does not give as clear an indication of the range of pentagonal shapes possible when the sides of the pentagon are rotated about its head, so here is an illustration of this particular exercise.

This simple animation has been created using arbitrary rotational intervals at the head of the pentagon of 3° to produce each of the shapes that make up the animation. The red and blue lines are merely there to indicate the separate sides of the shape creating the pentagon. The top angle contained by the red and blue lines is set at right angles. Note the areas contained by the two extremes of shape are a rectangle and a square, the rectangle occupying twice the area of the square.

This lower illustration is a simplification of the above animated drawing, the shapes here being established at 5° rather than the 3° rotations used above, and with the shapes resting on their bases compared with the animation.

go to top of page

A false five-pointed geometrical pattern

Recently I came across this particular pattern when reading about the life of Paul Erdős, a Hungarian mathematician of some significance in the different fields of his interests. I had at first thought it was a geometric construction and assumed, particularly, that each internal corner of the pentagon had been divided equally into four divisions.

Closer examination, and then an attempt to replicate it, showed that it was not based on an equal division of the internal angle but something quite different. More research turned up different versions of the same diagram where the construction line, dhfje, does not have connection lines following it, but has the point f veering towards g.

Further study informed me that the diagram has nothing to do with geometric construction, but is a representation of mathematical graph theory and shows the network connections between sixteen vertices or nodes, each connected in pairs to five other vertices, by five edges, or lines.

Nevertheless, I thought it an interesting pattern and have included this animation, though missing out the construction lines which divide each internal angle into four equal parts of 27° each. The animation shows the original pentagon with the blue construction lines illustrating how it might be changed with the pentagon’s internal angles equally divided.

go to top of page

Six point geometry

Six point geometry is by far the easiest geometry to construct, requiring only a simple form of compass to create the basis for accurate three-, six- and twelve-pointed forms. I have seen it drawn in Qatar and Iran using both a simple pair of wooden or metal dividers as well as with a string and two nails, one to fix the centre and one to describe the circumference. The string system can be used with nails, chalk or a stone to make a mark on a surface and the system tends to be used for larger circles. I should also add that, with a string and marker system, it is easily possible to draw simple ellipses, though this is very much a hit and miss operation and doesn’t really come within the area of these notes.

In order to construct a six-point design, draw a circle and, with the same radius, describe six circles centred on the points of intersection of each circle along the original circle.

Another way of constructing this geometry is by using seven mutually touching circles; a simple way of illustrating this is to place seven similarly sized coins so they are mutually touching. This geometry can be simplified or developed into three-point or twelve-point geometry respectively. However, as it requires solids to draw the circles, it is unlikely to have been used traditionally. Having written that, I have seen circular wooden templates lying around in Iran where I watched craftsmen setting out simple geometric designs, but I’m not sure how – or even if – they were used in this manner. The method I have shown here requires the centre diameter of each circle being drawn in order to fix the points of each corner of the hexagon.

An important characteristic of six point geometry is its relationship with √3. This first illustration sets out the simplest construction that establishes the basic √3 development. This would have been a simple geometry to establish with a piece of string and a straight edge.

A circle, when sub-divided by the superscription of six circles located equally along it circumference, establishes a right angled triangle with its hypoteneuse the diameter of the circle, and its shortest side equal to half the circle’s diameter, or the radius. The remaining side is, therefore, √3 times the radius of the circle.

In the lower illustration the rectangle with its short side coincident with two opposite sides of the hexagon has its long side in the proportion of √3:1 to the side of the hexagon.

The hexagon is one of the more important forms in Islamic geometry. It is simple to construct, it has the capability of producing, in repetition, an overall coverage of a surface, it contains the important relationship of 1:√3, and it bears a strong similarity to the circle, a symbol of creation in Islamic symbology. The hexagon, square and triangle are the basic shapes in this system, the square being associated with the earth and the triangle with human consciousness. In this manner it can be understood that there are a number of elements that would be apparent from an Islamic point of view.

go to top of page

A different six point geometry

Generally, the six-point geometry used as the basis of many Arabic or Islamic patterns can be seen to be developed geometrically as shown above and, here, to the side. It produces one of the most recognisable geometric shapes that is a feature of the design and artwork found in a number of cultures.

The lines forming hexagons or, here, a star can be seen to be derived from the junctions of circles of the same size which are set out on the circumference of a similarly-sized central circle. This is an easy geometry to construct requiring only a simple pair of compasses set to a single radius and a straight edge to join the points of intersection. But there is another way of constructing six-pointed stars which enables different effects to be obtained.

When six-pointed stars are constructed using the simple, traditional method, the external angles contained within the points of the star will be 120°. However, there is a simple construction which will produce external angles reduced to 90°. To illustrate the difference, here are the two different shapes using six-pointed stars of the same diameter. The internal angles of the points of the stars are respectively 60° and 30°. Note the very different characters of these two shapes.

Construction of this six-pointed star is not difficult though is different from the simpler hexagon illustrated above in that the central circle has to be divided into twelve parts in order to obtain the points on the circumference from which construction lines are taken.

Draw a circle and, with the compasses set at the same radius and the point of the compass set at a point on the circumference, divide the circumference into six parts by describing circles based on the common points of intersection. From those points of intersection draw lines that run through the centre of the central circle. The circumference of that circle will now have twelve points around it. From each of those points draw lines to the two points on the opposite side of the circumference. You will now have the basic lines upon which to draw the six-pointed star.

The geometry which is created by this alternative method gives another range of possibilities for making patterns based on six-point geometry. This pattern is the simplest way in which a pattern can be put together using only the six-point star, and creating an ancillary irregularly sided kite-shaped hexagon to fill the plane completely. This illustration shows the basic arrangement of hexagons, suggesting that the viewer is looking at a portion of an infinite pattern.

One of the characteristic features of Arabic patterns is the variety of alternative patterns found within them. Often these patterns can not be seen at the same time but appear and reappear as the eye scans. In the illustration above there are a series of circles created as hexagons that move in and out of focus. However, as shown in this illustration, the basis for establishing the pattern can be seen to be a series of pairs of mirrored 90° steps set at 120° to each other.

This sketch illustrates another characteristic of Arabic or Islamic patterns – the ability to create a variety of patterns based not on the shapes, but on the lines which contain the shapes. Here, for instance, the zig-zag lines have been broken down into a series of z-shaped elements which, when set out on a plane ground give the illusion of their weaving over and under each other. The underlying geometry of this pattern is exactly the same as shown in the patterns above, but the resulting effect is very different.

Here is another way of looking at the same or similar geometrical construction, but with the resulting of a simpler form of the hexagonal design. This is a construction that is commonly found in many areas where Islamic design has been used.

The initial setting out of the basic construction is similar to that shown above; draw a horizontal straight line and central circle from whose intersections first two more circles of the same diameter are drawn and then, from the intersection of the three circles, four more circles are drawn to complete the basic hexagonal group of six circles around a central circle. This pattern is then expanded outwards by another ring of similarly sized and developed circles.

Straight lines are added linking points of intersections of the circles and, from the intersection of arcs of the circles and the straight lines, a group of six irregular but symmetrical hexagons are created, enclosing a central star.

This basic configuration can be extended to form an infinite construction that is suited to the development of a wide variety of patterns. In particular, the lines forming its shapes are suited to create a sinuous line weaving its way within the pattern when there is little colour contrast between the lines and ground. When strong colours are used on the tiles, then a different appearance is created. In this crude illustration, the simplistic patterns created by the lineal form and the coloured tiles contrast strongly, though there will always be a tendency for the eye to read the lines of stars established horizontally and at 60° to the horizontal.

go to top of page

A development of six point geometry

Six-point geometry is found everywhere in Islamic geometrical work. This photograph, taken in June, 1975 in Shiraz, Iran, illustrates the wooden over-panel to a door, its patterning being based on six-point geometry. It is a relatively simple pattern and one which is not difficult to understand. Notice that the geometry has been established from the inside face of the trim forming the inner semi-circle, which leads to a visual design problem. Though this may not be the most sensible place to discuss it, the positioning of the springing of the curve defining the containing arch needs to be understood as it can look awkward.

This diagram shows a semicircle with a thick surround to it, similar to the over-panel in the photograph above. The springing of the arch lies on the inner edge of the surround which means that the the vertical line from the outer edge of the surround must drop from the point where the horizontal extension of the inner edge meets the outer edge, and not from the base of the surround as appears to be the case if you look at the right end of the surround. The pure semi-circle lies on the inner edge, not on the outer edge which, therefore, can not be a pure geometrical shape. While this is a digression, the point is relevant to many arches or over-panels where they extend downwards and where the eye can be confused.

With regard to its setting out, the above panel has been established with the larger rosettes placed at the junctions of a simple layout of six circles equally spaced along the circumference of a circle of the same size – shown darker at the centre of this diagram and set on the central, horizontal line. Two parallel lines are drawn as extensions to the top and bottom sides of the central hexagon, the lower one of these forming the base of the semicircular panel. Four vertical lines are drawn, two from the junctions of the outer circles, and two as tangents to the outermost two circles. From the centre of the bottom line of the hexagon a line is drawn to meet the junction of the outermost circles and central, horizontal line. This establishes the diameter of the semicircle.

This basic geometry set out above can then be used to produce lines along which the pattern can be developed. One of the easiest ways for a craftsman to be able to do this would be to continue drawing the interlocking circles as they will naturally produce the positions at their interstices through which lines can be drawn at 30° and 60° across the panel. Remember that the semicircle is established from the same base as the original hexagon, and that the line drawn horizontally through the centre of the hexagon cuts the semicircle exactly at two hexagon widths.

Establishing or setting a diameter for the larger rosettes was more problematic. It appears that their diameter might be set at a range of measures. However it is more likely that the diameter would relate mathematically to the geometry used to set out the basic framework. Looking at the original photograph in detail it appears that the trim around the larger rosette – the line which also trims two of the sides of each smaller rosette – actually follows the circumference of a circle, albeit in straight lines due to the wooden material from which it is made. For this reason it was decided to look at the smaller rosettes first.

Having established the centres of the small rosettes as lying at the centres of the equilateral triangles created by the interlocking circles, the next step was to determine their size. This was carried out by first creating the smaller rosettes which are six-pointed, each of the six element making them up being formed of a kite shape having internal angles of 90°, 60°, and two at 105°. Here is a corner of the panel. It may seem complicated but it really isn’t, the 15° angles being created by sub-dividing the 30° angles already formed.

In this sketch, all the small rosettes have been set out so that their pattern can be seen in relation to both the underlying geometry as well as the semicircular over-panel. What is evident is that there is a slight lack of coincidence between the semicircle and the rosettes. This has created a situation where five of the small rosettes are cut by the semicircle. If you look at the over-panel above, you can see that this is allowed to happen naturally with four of them left blind, but the top, central one amended slightly and appearing almost similar to the others which are glazed.

The construction of the first of the larger rosettes is relatively easily established by a similar process as was used for the smaller rosettes. In this case, many of the lines which define the larger rosette are set out by joining junction points, or points of change of direction, on the adjacent smaller rosettes. This sketch shows more of the construction lines than is necessary, but those establishing the larger rosette should be readily seen.

Here the small and large rosettes are shown in order to illustrate their relationship with the outline of the overpanel. While four of them are established on the baseline of the semicircle, another four are cut by the arc of the semicircle. The craftsman who made the panel has dealt with this neatly even though it has meant the incorporation of non-regular elements. Also note that the pattern of rosettes extends infinitely, the semicircle just incorporating a small part of that pattern.

There are many ways of presenting graphical studies of geometric Islamic work, as can be seen on these pages. This example is only one of many ways in which this particular design could be illustrated. Compared with the photograph of the over-panel shown above, this sketch has a lace-like quality about it which is at odds with the original, wooden construction partly due to the colours selected and the reversing of the image. It should be seen as a study of the geometry and not a replication of the original design.

Now for something completely different. Although this might not be the right place for it, here is a diagram which embodies an interesting characteristic which may, or may not, have associations with other areas of the arts or science. A correspondent has suggested that there may be a link between twelve-point geometry and Western musical notation. While I have not been able to persuade myself of this – and bear in mind that the general intention of these pages is to investigate geometry with regard to Arabic traditions – here is a diagram which illustrates how a circle, divided into twelve segments may be broken into two groups of five and seven segments, these being said to relate respectively to the number of black and white piano keys that make up the Western tonal system of music.

With its centre on a horizontal line, draw a circle and, at the intersections draw circles of equal size to the original, this being the basic construction for a hexagon. Halfway between the centre of the original circle and one of its junctions with the horizontal line, raise a vertical line. From the intersection of the horizontal and vertical lines describe another circle. This circle and the original will intersect at points which divide the original circle into five and seven parts.

Generally the patterns described on these pages are derived from geometric forms that flow seamlessly together, requiring only the selection and connection of those points of intersection that occur naturally in the construction of the basic geometries. However, patterns can also be established that take their design from other geometric forms and require only a specific location in the basic design to establish the key point from which the secondary pattern may be distributed.

The sketches here illustrate such a decision. The basic pattern appears at first glance to be based on six-pointed geometry, hexagons being easily seen to predominate the pattern. Yet the pattern here is based on four-pointed geometry.

go to top of page

A basic grid for six-point designs

This may not be considered a serious view of Islamic patterns, but the two animations are placed here to show how easy it is to produce a grid, based on six-point geometry, that can establish many points upon which shapes may be discovered and, perhaps, how a pattern might be formed within a circle. Extending the constructions would obviously enable larger patterns to be devised.

The grid requires a single line to be drawn initially upon which to base the circles that follow, the intent being to produce a circular shape in which a series of circular lines have been formed, creating a fine grid on which to base a variety of geometric shapes or patterns. In this way a compass can be used to describe the circles, their diminishing diameters being related in the proportions of 8:4:2:1. While the construction of the diameters have not been shown here, they are readily found though, alternatively, might be measured.

This animation begins by showing the grid resulting from the above construction. Composed entirely of curves, it has a very evident floral character to it, which is attractive in itself as a curvilinear design, but there is sufficient continuity and congruity in it that should allow many different shapes to be created using straight lines linking the intersections of junctions.

Overlain on the grid are a random selection of shapes that I believe are all different. In fact it is evident that more different shapes can be constructed with larger individual areas. Most of the shapes are regular, but there are a few irregular shapes too. No effort has been made to produce a regular pattern from any of them but it is obvious that there is considerable room for development of patterns based on any number or selection of the shapes.

go to top of page

Development of a six-sided design

Compared with the above method of producing a seemingly random group of shapes, here is a different and simpler way in which a regular six-sided shape may be developed to give the appearance of a three dimensional object – even without the addition of the shading that has been given to the final frame of the animation.

Begin by creating a regular hexagon. Draw lines interconnecting all its corners. Join the points of their internal intersections to create a smaller hexagon. From each of the corners of the large hexagon, draw lines through the corners of the smaller hexagon. There will be two lines from each of those external corners, here shown in light blue.

Next, draw the six lines indicated from the intersections of light and darker blue lines. This will create a hexagon slightly larger than the small hexagon. Following the setting out blue lines it is now possible to draw pentagons of two different shapes to create the impression of a three-dimensional dodecahedron. It is notable that there are lines of three different lengths creating this illusion.

go to top of page

Six-fold construction

It is quite possible that somewhere on these geometry pages there is something drawn similar to the example illustrated here but, if there is, I can no longer spot it.

However, I want to show here a traditional construction illustrated by Mohamad Aljanabi on YouTube which establishes the accurate setting out of a six-fold construction which he later compares with a very similar but more inaccurate construction which uses the grid method.

The importance of this construction is that it has elements which are naturally and accurately reflected, with no eccentricities in its relative proportions, lengths of lines or angles and is likely to be the same construction developed by traditional craftsmen in their development of patterns.

The construction of the underlying pattern of the sixteen amalgamated elements below begins with the drawing of a square, the construction of which is assumed for the purposes of the illustration which follows. Bear in mind this construction is for the top left corner of a pattern of sixteen.

With compasses set at the length of a side of the square and, centred on the bottom right corner, draw an arc linking top right and bottom left corners, then repeat this centred on the top right and bottom left corners. Next, draw the two diagonals of the square.

Now, draw lines from the bottom right corner through the intersections between the three arcs extending the lines to the top and left sides of the square.

Draw a line between the intersection of the first two arcs which joined corners, and the intersection of the two diagonals. With this line as the length of a radius, draw four quarter-circles centered on each of the four corners of the square.

Then, with the compass point at the junction of the lower diagonal line and the left side of the square, and radius set at its length to the lower left quadrant, draw a semicircle. Repeat this for the top of the square.

At the intersection of the two large arcs on the left of the square, and with compasses set at the length of the red line, cut the quarter circle in the lower left corner of the square. Repeat this action for the top right quarter circle. From the lower right corner, draw a line through that intersection to meet the diagonal, and repeat this action for the top right corner.

From the lower intersection, draw a horizontal line to meet the diagonal line drawn from the lower right corner. With the radius set at the distance of the junction of those two lines to the lower right corners, draw quarter circles in each corner. From the same junction, raise a vertical line to meet the small quarter circle at the top right corner. Now, draw lines from the junction of the first two large arcs to the lower left corner, and a similar line to the top right corner.

It is now possible to draw the pattern using this as the basis for the geometry.

go to top of page

Vesica piscis

It has not been my intention to look at sacred geometries on these pages. Nevertheless there are a number of designs falling into this category of geometry which have interesting constructions and can be found everywhere, though not necessarily in the context of sacred geometry. A case in point is the Vesica piscis – Latin for the bladder of a fish – which can be described as the shape created by the intersection of two equally-sized circles, each having its centre on the circumference of the other, and its width being that of the side of a square equal to the radius of the two circles. Extending the equilateral triangle to include the segment of the circumference of the circle produces a sector, one sixth of the circle.

The graphic above shows how the vesica piscis shape is readily created. The animation illustrates the addition of a small equilateral triangle created by joining the centres of each circle to one of their points of intersection – each of its sides being equal to the radius of the circles. As a consequence of this, the ratio of the height of the vesica piscis to its width can be seen to be in the proportion of √3:1. Coincidentally, this is the same ratio as is illustrated here – by connecting the diagonally opposite corners of a cube, that line will have the same relationship with the length of the side of the cube, √3:1.

go to top of page

Dividing a line into three equal parts

The construction of the vesica piscis leads naturally into an aside, the division of a line into three equal parts, clearly seen to be based on six-point geometry.

With compasses set to the length of the line, describe two arcs, each based on the two ends of the line. From their two points of intersection draw a line. This will bisect the original line in two and at right angles.

Place the compass point on the intersection of the original line and the second drawn at right angles to it and, with the compass set to half the length of the line, draw a semi-circle.

Now, from the two points of intersection of the original arcs and line, and with the compasses set at half the length of the line, draw two semi-circles.

These will intersect with the previously drawn semi-circle at two points and, from these points, draw lines back to the top intersection of the first two semicircles. Their intersection with the original line will divide it into three lengths.

go to top of page

Constructing an angle of 20°

Elsewhere within these notes there are references to the need to create an angle of 20° using only a pair of compasses and a straight edge. The angle of 20° and its sub-divided angle of 10° might commonly be required when dividing a circle into eighteeen or thirty-six segments. Two simple, similar alternative methods are described in this animated image; one follows the other.

On a horizontal line draw a circle from centre, a, with a fixed radius. With a centre on the point that circle intersects the horizontal line, b, draw a circle with the same radius. With centres, c and d, draw two more circles. Draw a line from the initial point, a, to the point, e, where the last two circles intersect. The angle created by ∠ade is 20°.

go to top of page

Seven point geometry

Seven point geometry is difficult to construct accurately – the internal angle of a circle divided by seven is 51.4285714° – though there is a relatively simple way of making an approximation which might be accurate enough within the normal working tolerances of traditional designers and craftsmen.

Perhaps, because of this basic problem and, particularly, the difficulty of combining other, simple geometries with it, I have rarely seen it used in Qatar. This first example was on a perforated naqsh carving in Wakra, which I photographed in 1976. Here it is with three seven-pointed rosettes and a five-pointed rosette at the top. It is obviously not a mistake. There is even a degree of symmetry along the bottom row of rosettes, though this does not carry through to the top rosette, nor to the links between them. There are two more examples on one of the Gulf architecture pages. Those are fourteen-point examples, but are obviously based on seven-point geometry.

With its centre on a horizontal line draw a circle and, with the centres on their intersection and the same radius, describe two arcs which cut the circle. Draw two vertical lines from the points of intersection. Construct a third, vertical line bisecting the circle. From its point of intersection with the circle draw a line which meets the junction of the horizontal line and circle. This line will be at 45° to the horizontal line.

Now, with its centre on the intersection of the first arc and the circle, describe an arc from the point where the line joining the 45° line cuts one of the two vertical lines. The length of one of the sides of the heptagon will be from the point where this arc cuts the circle to the intersection of the central, vertical point of the circle. The additional points of the heptagon can be located by describing arcs with radius the length of this line.

Just as there are with many other geometries, there is an alternative construction which again gives a good approximation of a heptagon – certainly one that can be used for the usual degrees of accuracy likely to be required for small scale patterns.

Begin by drawing a circle – shown here, dark blue – and then continue drawing six circles with the same radius around, and centred on, the circumference of that circle. This is the same construction as is used to create a hexagon. Join every second junction on the circumference, producing an equilateral triangle. Where the two sides of the triangle cut the top peripheral circle, draw a line joining them to form a smaller equilateral triangle.

Now, with the compasses centred on the same position on the circumference as was used to create the first of the circles on the circumference, draw a circle – shown here light blue – which has the bottom of the smaller triangle as its tangent. This smaller circle will cut the initial, central circle in two places. With compasses set to the same radius, continue to draw circles centred on the circumference of the original circle, but with the new, smaller radius. This will divide the circumference approximately into seven.

Here is another way of creating an approximation of a regular seven-pointed shape.

Draw a circle with compasses centred at the intersection of a horizontal and vertical line. With its centre at the junction of the circle and vertical line draw another circle of the same radius. This circle will intersect with the first circle at points b and c. Joining these two points with a straight line will create an intersection with the vertical at d.

With compasses set at their centre with point a and radius bd describe a circle which will intersect with the original circle at e and f. With compasses centred on these two points, and with the same radius, describe two more circles which will intersect with the original circle at g and h. With the compasses centred on these two points, describe two more circles of the same radius, intersecting with the original circles at points j and k respectively. The seven points, a, e, f, g, h, j and k locate the seven points of the regular heptagon.

As with the previous two methods, this also creates a slightly inaccurate heptagon, the length of the side at the base – j k – of the shape being approximately 1.25% longer than the lengths of each of the other six sides. It should be possible to create a more accurate regular heptagon, but only by inspection and experimenting with the radius of the smaller circle used in establishing the corners of the heptagon.

While it may not be related to constructional complexity, seven-point geometry has an importance in some religions. This example of the use of seven-point geometry is the blue granite fountain and surrounding pattern within the entrance to the Ismaili Centre in Kensington, London. The pattern is reflected in the ceiling and represents the seven pillars of Ismailism, a development of Shi’a Islam’s five pillars by the addition of walayah, guardianship and jihad, struggle. The entrance area has seven columnns and, elsewhere in the building, a seven-sided shaft is used to introduce light to the ground floor.

Elsewhere I have noted that one of the characteristics of patterns created on the basis of an odd number of points, is that the points may be joined by a single continuous line. This enables a typical device to be used – the notional or actual interweaving of the line under and over itself as can be seen in the photograph of the fountain above. This works only where the lines are contained within, or projected beyond the basic heptagon – shown in this diagram as the heavy red line. Where the lines are extended, a decision has to be made by the designer in fixing the outermost points of the pattern. Usually this can be organised in relation to a projection of lines within the central device. In this diagram the centre points of each side of the heptagon have been joined by a line that has been extended to meet the adjacent extended lines. This creates a series of positions that relate naturally to the constructional geometry of the heptagon, and appears to be the method used in the fountain design. I have yet to try and determine the setting out of the surrounding floor pattern.

Having noted previously that I had never seen any example of seven-point geometry in Qatar, I have come across a photograph of a modern carving, fashioned in wood, that is based on seven-point geometry, there being fourteen blades to the pattern. This illustration is a relatively accurate representation of it, the purpose of this exercise being to investigate how the pattern might have been set out. On the original carving, the circles and the lines of the blades have been scored in the wood with the recesses between them carved out.

The first thing to notice about the illustration is that the design spirals anti-clockwise, in common with the majority of spiral designs seen in Qatar in the past. This feature has been commented on elsewhere and examples of traditional spirals carved as naqsh plasterwork on one of the other pages looking at different aspects of Arabic geometry, this one relating to traditional designs in Qatar.

This design has two areas of interest in its construction. The first is in determining how the curves of the blades are established, the problem being to establish where the centre of the first blade might have been located, and what its diameter was. The second relates to the curious design of the short trailing edge of the blade and its unusual connection with the leading edge of the following blade. It has not been too difficult to establish how this was set out, but why it should have been designed in this way is impossible to know and unlikely to have been an element of traditional designs.

It should be assumed that while the diameter of the spiral blades and the first centre can be established, the positioning of subsequent centres is not possible unless the approximating method illustrated at the head of this section is used, it being impossible to create an angle of 25.71428° easily. It is most likely that a simple method of stepping out the subsequent thirteen positions for their centres would have been carried out by trial and error, essentially an iterative process.

Using the central of the three concentric circles – shown in white – raise a vertical line from the junction of the horizontal line with the circle (a) as well as from the centre point midway between that intersection and the centre of the circle. The point at which the latter vertical line intersects with the circle (b) will be the centre for the first circle, shown in red, which establishes the first blade of the spiral. This circle is the same diameter as the original, white, circle.

The red and white circles intersect at two points, (a and c). Draw a line through these two points extending it a little. This is the line which establishes the short trailing edge of the spiral. This extended line as well as the sixth similar line will intersect at (d). This intersection establishes the diameter of the outer circle of the design. In order to establish these lines, as well as the position of the blades of the spiral, the initial circle and line have to be repeated around the circumference of the original circle using the trial and error method.

go to top of page

An example of seven- or fourteen-point geometry

As noted above, the application of seven-point geometry is relatively rare but occasionally is spotted in odd places. A photograph taken inside a mosque in the old Islamic quarter of Cairo shows an eccentric arrangement of what appear to be three square panels, the lower two based on ten-point geometry, the upper one in fourteen- or seven-point. Apparently constructed at a single time, the upper panel has no real relationship with the lower two, nor do I understand how this might have come about. Note that the nature of the geometries used in the different panels means that neither the ten- or fourteen-point panels occupy a square.

Here is a rough illustration of the decorative panel above showing its proportions approximately correct. The fourteen external kite-shaped petals of the central element of the panel can be seen to touch the petals of similar fourteen-point figures outside the corners of the panel with two of the central figure’s petals being free – not touching the external figures – at the top and bottom, and three of the petals being free on the left and right of the panel. The orientation of the external, four corner figures is the same as the central figure of the panel.

This lower illustration shows the elements of the central figure of the panel together with the four located outside the external four corners of the panel.

Possible construction lines have been included in this diagram, but they have to be considered tenuous for a number of reasons. The main two points are that, firstly, there is no accurate way of constructing a seven- or fourteen-pointed star, as mentioned above and, secondly, the exact shape of the petals is dependent upon a number of decisions that will have been made by the designer of the panel, and these can only be guessed at by a close inspection of the panel. In particular, the point at which the internal lines cross in forming the fourteen petals has an effect on the shapes of the internal four and six sided kite-shaped petals, indicated in colour in the top right element. Variation to the parallel lines that create opposite pairs of petals within each design, will alter their crossing points.

These variations to the distance apart of the parallel lines indicate something of how the four and six-sided kites that form the petals can be varied. In this diagram, the parallel lines have been placed between different intersections of the fourteen circles that were used to establish the basic fourteen-pointed figure. Only three variations have been shown here, but of course other possibilities exist. Bear in mind that there is bound to be a degree of inaccuracy due to the difficulties of constructing an accurate heptagon.

go to top of page

Eight point geometry

Marginally less easy to construct than are six-point geometries, designs based on eight-point geometry are readily created with the use of just a pair of compasses and a straight edge for their construction. Designs based on eight-point geometry are seen to have an important resonance in that there is reference to their character in the surah al-haqqaah of the Holy Quran:

And the angels will be on its sides, and eight will, that Day, bear the Throne of thy Lord above them.

which suggests that there might be a tendency to use it more often than other basic geometries. While I have found no evidence of this, it is not impossible to believe that there might be a preference to use it in the selection and application of designs in certain settings.

Probably the easiest approach to the construction of an octagon begins in exactly the same manner as it might be with a square set out with four point geometry – albeit with the square set on the diagonal – at 45° to the horizontal.

Using a pair of compasses set at a fixed diameter, draw a circle with its centre on a horizontal line. From the two points that circle cuts the horizontal line, draw two more circles each having the same diameter as the original circle. Through the points where the outer two circles intersect, raise a perpendicular through the centre of the original circle. When the four points where the horizontal and vertical lines intersecting the central circle are connected, a square will be produced, but set on the diagonal.

With centres at the points where the vertical line intersects with the central circle, draw two more circles of the same diameter as the previous circles. From the points where these two circles intersect with the original two outer circles, draw two diagonal lines. The central circle will now be divided into eight equal lengths along its circumference, creating an octagon.

This graphic pattern is similar in many respects to the twelve-point spiral pattern that is illustrated on the preceding page of these notes. The graphic illustrates how a basic geometric framework, developed from simple four- or eight-point geometry, might be evolved to create a secondary framework suited to the development of different patterns that maintain a similarity to the originating geometry, but allow for subtle change in the character of the developed pattern.

The pattern is based on an initial stacking of nested squares, each half the area of the previous one – established by using the centre point of each diagonal – and then joining the corners of other squares. It is significant to note that not all construction lines are coincident, but allow for subtle differences to the artist developing a pattern; though only one solution is shown here. The final pattern, like the twelve-point spiral pattern referred to above, has a strong direction implicit in its design, which can be read either clockwise or anticlockwise. Note that the eight-point spiral is significantly less subtle than the twelve-point spiral on the previous page, it following that the more points used, the more refined the spiral will appear.

This animation shows another simple way of constructing a basic eight-pointed design which can be tiled or developed with other elements to create constrained or infinite patterns.

Begin by constructing a square – the construction is not shown here but can be readily found on this page or elsewhere. Within it add the diagonals and central horizontal and vertical lines which will enable a circle of the same diameter as the sides of the square to be drawn.

Add horizontal and vertical lines at the intersections of the diagonals with the circle, then draw a square at 45° to the containing square, its corners being located at the mid-points of the containing square. The circle can be seen to have eight equidistant points along it. Draw lines from each adjoing pair and extend them to meet or intersect with the containing square.

The 45° square is intersected by the square which can be seen to have its corners at every other point on the circumference of the circle. From those eight points of intersection draw and extend horizontal and vertical lines to meet or intersect with the containing square.

The lines indicating the elements of the basic pattern are shown in the above animated illustration as red lines. The outlines of two crosses can now be drawn on the red lines, the cross at 45° having its ends extended to meet the containing square.

The resulting octagonal pattern can be used in a variety of developed patterns, one of which, infinitely extendable, is demonstrated here, with the octagons approximately a quarter of the size of the animation above.

The pattern immediately above is one of the more commonly found examples of this simple development of eight point geometry. Other patterns – a small number illustrated here – can be found where the eight-pointed star has been developed using colour variations within the segments of the star’s lines. Note that the outline of the star can be generated by overlapping two crosses, mutually rotated at 45° to each other – shown in the two images top right – or by a single continuous line.

This pattern shows some but not all of its construction lines, and is a rough illustration intended to describe something of the construction of the pattern shown two diagrams above. Construction should be possible from this diagram. Note that the pattern is shown here set out at 45° to that coloured pattern.

This appears to be the easiest way to draw the pattern. Note that the width of the parallel elements, the lozenges, which define the eight pointed star are established by the width of the small octagons.

However, recently I saw another illustration of the pattern, but noticed that there was a slightly different way of setting out the width of the elements which make up the eight pointed star.

Within the large circle draw a square which will have its corners at every other corner of the octagon. With compasses set at the centre of the circle, describe a smaller circle which will have the sides of the square touching it at tangents on all four sides. The long sides of the four lozenges which make up the star within the octogon will be drawn with their long sides intersecting with the circle. It will be seen that this creates lozenges slightly narrower than those in the first design.

There are many ways in which the basic octagon can be defined using points or lines within the pattern to establish them. This diagram shows four ways in which the star within an octagon can be developed with lines from the two patterns immediately above, allowing patterns, such as that foour illustrations above, might be developed. Note that in the case of all these octagons that the sides of the lozenges creating the star are always parallel. It is possible to amend this for more variations to be created, perhaps making an overall pattern more lively.

This diagram illustrates a small number of alternative patterns which can be constructed if the lozenges creating the octagonal star do not have their long sides parallel. On the top left, and below it, are the original octagonal star with parallel sides and, to the right are two stars where the ends of the stars are fatter, then thinner with, on the right, where the ends of the stars are fatter but create a spinning effect.

more to be written…

go to top of page

A development of eight point geometry

There are only two regular two-dimensional shapes that will stack closely with no space between them – the square and the hexagon.

Much of Islamic geometry depends upon patterns composed of more than a single type of geometry, the linking elements being developed in relationship to the basic shapes used. These are usually based on the lines related to the construction of the simpler geometrical shapes, hidden within them, so to speak.

But some of the shapes have a simple link possible – in many cases a triangle and rhombus. The octagon will not stack as do the square and hexagon, but there are two types of pattern formed by relatively simple linkages. In the upper of these two examples I have turned the octagon through 22.5° and then added squares which have sides the same length as those of the octagon. Although there is a symmetry to this pattern on a large area of repetition, the pattern radiates from the central octagon outwards. Compare that with the second pattern below.

In this case the octagon has not been turned but balances on a point as in the construction above. This creates a more dynamic shape than in the first pattern above. The difference between this and the pattern above is that this is symmetrical in two dimensions. Its other characteristic is that it brings in an implied circular pattern that the eye reads, introducing a flow to the pattern. Both patterns are found commonly in Islamic design but it is interesting to note that the lower pattern is being incorporated into the façade of one of the buildings in the New District of Doha.

go to top of page

A more complex eight point geometry

The investigation above of an eight-point geometric design illustrates a relatively simple design whose underlying geometry is neither difficult to understand or replicate. Sometimes more complex patterns are found which appear tp require more time spent on them in order to see how they were constructed, but which may throw up interesting aspects relating to their geometry.

This design, which was found on a very interesting site dealing with the complex three-dimensional geometries of a theoretical project, caught my attention as it seemed to be different in character from much of what I had seen in Isfahan, the name by which this site is characterised. This upper pair of graphics are part of a sequence describing the development of a fountain floor pattern, the lower graphic illustrates the underlying geometry upon which the design was developed. My interest was two-fold. Firstly, that the design had strong similarities with Celtic designs and, secondly, that it seemed very different from Islamic geometries previously looked at and, in particular, a more modern interpretative design solution.

While the design had an obvious basis in eight part geometry, its method of construction was not immediately obvious. This lack of clarity was initially reinforced when examining the first diagram, shown here, which established the underlying geometry, but which did not define the relationships either between the centres of the circles, the relative sizes of the two circles nor the width of the interlacing line.

The following sketches were an attempt to understand and establish the underlying geometry. Consider them to be a best guess.

The first point to make is that the completed design has a width to the interlacing line, the setting out showing both edges of the line as well as a dotted central line. A line drawn between the centres of the two circles does not form a tangent to the dotted circumference of the larger circle, though it does to the outside of the interlacing line as is illustrated here. Measurements across the circles show them to be in the proportion 18:29, but the most significant discovery is that the angle subtended between the centre of the large circle and the two small circles – was approximately 70°, an angle which can not be constructed with ruler and compass.

This animated graphic illustrates how the setting out, shown above, is likely to have been established. However, one thing should be borne in mind, and it is that this graphic bases its geometry on a relationship between the lines forming the outer circumference of the large circle and the central circumference of the small circles as this appears to be the only way in which the design can be created. If this is correct – and it would be the first time I have come across this method of creating patterns – then it would be unusual in traditional geometric pattern making.

The other point to make has been mentioned previously but is worth repeating.

With this construction it is possible to create an approximation for the angle of 35°, an angle which is not capable of being constructed with ruler and compasses. From that, other angles can be constructed by the addition or subtraction of simpler angles such as 30° and 45°. In this way approximations for 5°, 10°, 65°, 70° and others can be constructed.

It can be seen that CD’B’ is an equilateral triangle, the line AC cuts the vertical raised from B’ at C’, and that the triangles ABC and AB’C’ are similar.

This establishes the length of the line h’ in relation to the radius of the circle.

The angle θ in the triangle B’D’C’ is given by tan θ=h’/R. Therefore the angle created is

θ=arctan(2√3/5) or 34·71500°

go to top of page

Nine point geometry

Although it may seem counter-intuitive, it is not possible to construct an accurate nine-point geometry. However, there is a method for making a good approximation.

First of all construct a six-point geometry within a circle as described above – by drawing a circle and, with the same radius centred on the circumference of that circle, draw six more circles. Join the intersections to produce a six-pointed star comprised of two interlocking equilateral triangles. Run a vertical line through the centre of the circle. From the point where that vertical line meets the horizontal line of one of the triangles forming the six-pointed star, draw a circle whose radius is half that of the original circle. With the same radius draw another circle with the centre on the junction of the vertical line and original circle. Where the those two similar circles meet, draw a horizontal line. This line will cut two of the sides of one of the equilateral triangles which form half of the six-pointed star.

From these two points of intersection, draw lines to the two points where the other equilateral triangle meets the horizontal side of the first equilateral triangle, and extend them to cut the original circle. The points where they cut that circle will be a very good approximation of a ninth of the circumference. With centre on one of the points of intersection with the circle and radius at the other point, draw a circle to cut the original circle and continue this around the circle to divide it into nine parts. Join these points of intersection to produce the nonagon.

The nonagon is an interesting development and occurs in many Islamic geometric patterns. This diagram, an extended nine-point rosette, is created with a single line joining the points on the circumference of the original circle, the line to be followed being found by the addition of lines joining the alternating points on the circumference.

There is, however, another possible construction. Found on a website dealing with sacred geometry, it’s not clear to me if this is anything but another approximation, but it is certainly interesting. Its beauty lies in its requiring only compasses to establish the nine points of a nonagon. As such it is quite possible that it would have lent itself to designers as a simplistic means of establishing a nonagon suited to most constructional requirements.

Draw a circle and, with the compasses set at the same radius and their point on the circumference, draw a further six arcs each cutting the circumference, their centres at their mutual intersections on the circumference. This will establish the corners for a standard, six-pointed hexagon.

With the compasses set at each of the corners of the hexagon, describe six arcs, each joining the opposite pair of equidistant corners. These arcs will create a hexagonal star, but with curved intersecting edges.

With the compasses at the point of intersection of each pair of arcs, and their width set to the corners of the hexagon at its maximal width, describe arcs joining those corners.

Now, with the compasses at the centre of the hexagon, describe a circle whose radius is established by the intersection of the previous arcs.

With the compasses set to that radius, place them at one of the points of the hexagon on the outer circle and describe a running sequence of arcs intersecting with that circle. This will create the positions for the corners of a nonagon.

go to top of page

Ten point geometry

There are a number of ways of making a ten-point geometry, and I have amended the original drawing I made earlier to suggest what I believe is a simpler method.

With this method, first construct a pentagon as has been described above. With this as the basis, next find the centre of the pentagon by raising a perpendicular from the centre of each of the five sides of it. This is effected by drawing arcs, centred on the points of the pentagon, above and below each side of the pentagon. The junctions of these perpendiculars will give you not only the geometrical centre of the pentagon, but also an additional five points at their junction with the super-inscribed circle. Joining these points with the original points of the pentagon will give you the ten-pointed figure.

Just as there is with the nine-point geometric construction, there are a number of ways to develop the patterns used in Islamic geometrical work. Two are shown here. In the left hand diagram here, the straight red lines show how the internal points of the star are located and, again as with the nine-point star, the complete ten-point star is created with a single line. The right hand diagram illustrates another common construction, though here the star is made up of five similar patterns rather than a continuous line.

The geometrical construction of a ten-point pattern shown above is only one way in which a simple decagon can be drawn in order to create a different basic pattern which might be developed into an infinite pattern suited to cover a two-dimensional surface.

The animation shown here is essentially the same as that which is developed in the first diagram above, but the resultant decagonal pattern is developed in a slightly different and simpler way.

The decagonal star here can be compared directly with the decagonal pattern immediately above to the right and can be seen to have a very different character, essentially having a significant undecorated area within it and, compared with it, not being drawn with a single line, but two.

There are many ways in which patterns have been developed on the basis of 10pt geometry, some of them shown below and on other pages. The basic construction of the decagon has not been shown, but here is a graphic of a rosette based on this form of geometric – with the same orientation as the rosette above –All the time showing the construction lines used in developing the pattern as well as many which are not needed but illustrate something of the underlying structure from which a variety of rosette patterns might be investigated and constructed. It can be seen that the underlying links between the ten points on the circumferences can be used to develop a variety of shapes all based on the underlying symmetry of the decagon.

go to top of page

A development of ten point geometry

Here are two other ways of using the simple ten-point pattern illustrated above. The pattern on the left is a simple ribbon development showing the geometry as a single plane. That on the right has both an applied shadow to give it something of a three-dimensional feel to it, but also has the ribbon inter-leaving itself as it moves around the geometry, a form that is sometimes a feature of two-dimensional geometry when there is a wish to elevate the design.

Although it was intended that the above two patterns should be read separately, and that they represent two different concepts, in putting them together in a single diagram it is noticeable that there is an implied relationship in their almost touching. Despite the two patterns’ conceptual differences, there is a strong feeling of natural attraction that suggests they should touch or even be linked. This is a natural consequence of the manner in which our brains react to visual stimuli and attempt to form more understandable patterns. It is a characteristic of our brain that operates all the time as it processes what our eyes feed to it.

With regard to the joining of patterns it is evident that the different types of geometry have the ability to make natural junctions, continuing the geometry to create an infinite pattern, bounded only by the borders of the object in which the geometry has been established. These three illustrations demonstrate how a simple horizontal shift of the basic rosette shown above, enables different geometric patterns to be brought into effect. There are other ways of joining the patterns, but these three examples are the main ways in which ten point geometries join naturally, as can be seen for two of them in the diagram below.

Patterns based on geometries that are not symmetrical about both their horizontal and vertical axes will not be able to create regular patterns in both directions. Essentially this means that only four, eight and twelve point geometries have the property of two-directional pattern symmetry within them, whereas six and ten point geometries will have different joining properties with regard to horizontal and vertical directions. In this diagram you can see two of the natural joining relationships for ten point geometry, and how the vertical relationships differ.

And here the relationship between the three rosettes is not based on the coincidence of the main lines of the pattern as is true for the diagrams immediately above, but of the centres of the rosettes with those lines. Note that the relationship between the corners of the two top rosettes with those of the lower one are not the same. This is one of the characteristics that allows for a degree of diversity and invention on the part of the designer, and leads to the apparently infinite number of patterns found in Islamic designs. Let’s look for a minute at the construction of just one of these relationships.

The pattern on the left of these two illustrations is the same as above and to the right. The additional lines show how the lower of the three rosettes is positioned. In order to position the third rosette, extend the two, angled, oblique lines from the outer edges of the two upper rosettes to meet and then further extend them to cut perpendiculars dropped from the two centres of the upper rosettes. Where they cut, a horizontal line is drawn between them. A line dropped at right angles from the centre of the two upper rosettes will bisect the horizontal line, this point being the centre of the third rosette.

Note that, in the illustration on the right, the relationship between pairs of lozenges – one in the lower and one in either of the upper rosettes – a line drawn between them has the respective lozenge lying on each side of that line. This brings up the issue of the manner in which underlying geometry is used in delineating patterns.

The ten-pointed rosette is an extremely common feature of Arabic patterning. The construction shown above illustrates how the individual rosettes may be moved apart in order to create relationships capable of being developed into differing pattern effects. The third pattern down shows two rosettes with their inner rosettes touching each other. When these two rosettes are turned through 60° as shown in this first diagram, they can be developed into what is probably the simplest of patterns employing solely ten-point geometry. For the majority of these patterns, the ten-pointed rosette is combined with other rosettes based, commonly, on five or six points. This pattern, however, does not rely on these complications but is the simplest construction based solely on the decagon.

If you look at the pattern here, at first sight it appears to be composed solely of decagons touching each other, though this is, of course, impossible. With the addition of some simple shapes, shown shaded in the illustration above, a six-sided lozenge – the same element as is found within the rosette – a series of five-pointed stars and another six-sided shape, this time derived from three of the points of the five-pointed stars, the ten-pointed rosette can be developed as an infinite pattern with a simple, lace-like quality due to its relative simplicity.

The second diagram, immediately above, shows something of this quality in a single-lined illustration of the first diagram. The third diagram, here, gives a little width to the stroke and, with the aid of a drop shadow, suggests the quality of a pattern that might be constructed as a mushrabiyah screen, a common feature fabricated in a number of materials, and at different scales, throughout the Arab world, and used as a brise soleil, a device providing different degrees of privacy, or both.

The lowest illustration of this pattern in use is a photograph taken in a new museum in Abu Dhabi. Here, a large screen provides a degree of privacy and control of the view both in and out through its openings. Screens such as this commonly have considerable thought given to the relationship between the voids and solids in the design, not only in their widths, but also in their thicknesses. In addition to which their colour and profile has to be considered in order to obtain the optimal performance requirements of the screen.

This animation illustrates another way in which a ten-point rosette can be constructed, this time with a series of ten regular five-pointed stars rotated around its centre. The first part of the pattern, the construction of a ten-pointed star has been for the most part omitted, but a method can be found at the beginning of this section.

The process begins with the construction of a pentagon with sides the length of the first horizontal line drawn here. The pentagon is then rotated through 36° in order to produce the decagon. The method described above requires the construction of lines raised vertically with respect to the centres of each of the five sides of the pentagon, but is not shown in this animation.

With the ten points of the decagon established on the circumference of a circle, lines are added linking all those points. A point is now established at the intersection of one of these linking lines which joins two of the corners of the decagon having one corner between them, and two which have two corners between them. With a radius established from the centre of the circle to this point, a circle is described that will intersect with the decagon in twenty places, each pair on either side of a diagonal drawn through the centre of the circle.

An alternative way to define the five pairs of lines would be to identify the twenty points around the rosette as described in the paragraph above. Linking these points will establish the guides to identifying and drawing the pattern.

go to top of page

A different character of ten-point geometry

Most of the designs illustrated on these pages have to do with Islamic or Arabic geometry, or related studies. However, as this part of the page looks at ten-point geometry, it might be worth illustrating a design based on ten-point geometry, but which is patently un-Arabic in its character in order to point up at least one distinction between them. This first sketch shows a ring of ten circles touching at a common point. I have not shown the setting out of this grid, but it can be subsumed from the construction above.

On the page looking at Qatari naqsh there is comment on the spinning motif used as a decorative element. That was developed in the same way as shown immediately above, though the number of spokes to the motif varied, and the spokes were often unequal. However, the purpose here is to show a spiral constructed by first developing a shape by selection of lines from the pattern – shown above – and then – below – spinning it around the design, reducing its size by 20% each full rotation.

These first two diagrams share exactly the same geometry. The only difference between them is that there is a slight variation in the way in which the basic shape has had its colour gradient shaded. Whereas the diagram on the left of this pair appears symmetrical, that on the right shows significant movement by virtue of the shading being made to the side of the basic shape and not to its outside edge as in the diagram on the left.

Here is a variation of the same pattern as is used above, but this time coloured. The two designs are, in fact, the same, though that on the right has 50% transparency in order that I could investigate the wa in which the colours would bleed through. The colours are arranged in conformance with the colours of the rainbow and their diminishing sizes and attraction to the centre can be clearly seen compared with the sketches above. The point to make is that these patterns, while notionally sharing their geometry with traditional Arabic patterns, do not look Arabic. The main reason for this appears to be due solely to the variation in size of the patterns. But make your own minds up…

go to top of page

Eleven point geometry

While there are many examples of patterns created on the underlying basis of geometries based on three, four, five, six, eight and nine divisions, it is relatively unusual to come across patterns based on eleven.

Dividing a circle into eleven equal parts is not easy to accomplish with simple tools, though one possible construction is set below. This difficulty may be the reason for the apparent dearth of eleven-based designs. But from time to time it is possible to come across a design which is based on eleven-point geometry, such as is the case illustrated by this plate. Whether here it was a deliberate or an accidental design decision, is hard to decide. I suspect it was a considered decision, but why that might have been so I have no idea.

The plate was spotted displayed in a shop window, its central design being clearly based on eight-point geometry with a design vocabulary of flowers and leaves. The central design character can be seen to be quite different from the surrounding designed ring. Although the left side of the plate is partly obscured by the handle of a matching jug, it is quite easy to see that the outer ring of its design is clearly set out with eleven point geometry. There appear to be two orientations where the patterns might be seen to coincide – at approximately four o’clock and, perhaps at twelve o’clock.

With regard to the construction of eleven-point geometry, you should be aware that there seems to be considerable confusion about the name of the eleven-sided polygon; I understand it to be the hendecagon.

Eleven point geometry relates to one of the polygons that are not constructible; it is not possible to form such a polygon using only an unmarked straight edge and compasses. There are, however, a small number of rather complicated constructions that will produce a relatively accurate eleven-pointed polygon which may be found by searching online.

However, this first construction was based on a piece of origami work suggested by a Professor Dutch, which seems to have disappeared since I wrote this original note. However, another origami construction has appeared and can be found here, though this graphic is a re-drawing of the original, and illustrates a method of producing a regular hendecagon, and appears to be a relatively accurate way of constructing the internal angle.

Sub-dividing the large square three times consecutively along its diagonal produces a point on the edge, ‘A’, to which a line is drawn from the centre of the square, ‘B’.

Bisect ∠ABC to obtain ‘D’.

Next, bisect ∠EBD to obtain ‘F’ and then bisect ∠EBF to obtain ‘G’.

At 32.73373720°, the angle ∠EBG is a very close approximation to 32.72727272°, which is the internal angle of a hendecagon.

Repeating this angle around the centre, ‘B’, and superimposing a circle, enables you to draw the points that create the hendecagon.

go to top of page

A development of eleven point geometry

The reason I have chosen to construct the hendecagon in this manner, following the work of Professor Bodner, is that it is part of a process by which she recreated a pattern from the important Topkapi scroll that incorporates eleven point and nine point geometries, both of them unconstructible. A second point to note is that the rectangle upon which the two geometries are constructed does not locate the centres of the eleven and nine point geometries at its corners, as is common with Islamic patterns, but upon its edges.

Subdivide each of the sides of the hendecagon. From these eleven points, together with the eleven points of the hendecagon, connect to every ninth point around the polygon. In effect this draws a continuous line from a point of the hendecagon to a point on a side, to the next, ninth, point which will again be a point on the hendecagon, and so on – a,b,c,d,e… Following the lines that connect only the points on the sides of the hendecagon and linking them to every other central point, you will arrive at the star shape illustrated on the right.

In order to develop the pattern, the eleven-sided polygon has to be repeated and, in order to locate it, a rectangle has to be established on which it will be positioned. To do this, extend a vertical line through the centre of the right-hand polygon and draw a circle equal in radius and congruent with the circle describing the right-hand polygon. This forms the right hand side of the rectangle. From the centre of the top circle, extend a line left which will form the top side of the rectangle.

Next, establish the left and bottom sides of the rectangle by extending three lines from the centre of the right-hand polygon, the top one of which will intersect the top side of the rectangle. From this point of intersection, drop a line at right angles to the central of the three lines previously drawn from the right-hand polygon, and extend it to meet the lowest of those three lines. That point of intersection lies on the bottom line of the required rectangle which is formed by constructing a line at right angles from the vertical, right hand side of the rectangle. From the point where the central line and dropped line meet draw a circle with radius set to the centre of the right hand eleven-sided polygon. At the point of intersection of the central line and circle, construct a line to form the left hand side of the rectangle. At the point of intersection a second, eleven-sided polygon should be constructed.

As you can see from these sketches, the construction of this pattern becomes a little more complex now. Should you be interested in step-by-step instruction of the design, I suggest you look at the original article from which I developed my illustrations. The sketches I have placed here are not sufficiently detailed for them to be followed here but are placed in order to show not only something of the difficulty involved, but also to suggest that the method works, and that it would have been possible for the Topkapi illustration to have been constructed.

This last sketch in the series is as far as I will take the illustration of this construction as I have to admit I found it difficult to obtain the degree of accuracy to which I usually draw. However, that is not a criticism of the method, rather a comment on my drafting techniques.

So, here we have the reconstructed pattern from the Topkapi manuscript or, more accurately, a version of it drawn to produce a reasonable understanding of the basic rectangle with its associated eleven and nine point geometries.

The reason I have taken the trouble to set out this design in some detail above is both for the difficult nature of its construction as well as for the lively character of the pattern produced by using the two geometries together, most probably a function of combining the two odd-numbered geometries. Note that the two eleven-point stars on the left and right are mirrored with respect to each other on a horizontal axis, as are the nine-point stars at the top and bottom which are mirrored on a vertical axis.

This pattern has been created by extending the basic rectangle. This has been effected by mirroring both horizontally and vertically in order to have the pattern run through coherently. The result is a gently undulating pattern, perhaps dominated by the larger eleven-point star due to there being more white space within it compared with the nine-point star. But that is one of the characteristics of Islamic patterns, where balance is sought within an apparently infinitely extendable field, but where interest is created by point and counterpoint.

Finally, although the intention of this note has been to set out the construction of the hendecagon, this construction has been placed here in order to illustrate a simplistic pattern treatment of eleven point geometry by the interleaving of lines that connect all points around the circumference of the hendecagon. Compare and contrast it with the pattern set out above.

With an uneven number of points there will always be parallel lines visible – in this case four lines that can be seen to rotate around the centre of the hendecagon – 1 and 10, 2 and 9, 3 and 8, and 4 and 7. But what is significant in pattern making here is that the lines joining the eleven points are just capable of passing each other so that the appearance of an interleaving pattern may be established, albeit with relatively narrow colour strips.

go to top of page

Twelve point geometry

Twelve-point geometries are not that difficult to set out geometrically, and can be readily constructed by reference to three-point and four-point geometry constructions, both of which are easy to construct with compasses and straight edge, their construction being found elsewhere on these pages. Patterns based on or including twelve-point geometries are very common and lend themselves to sub-dividing as twelve can be divided by two, three, four and six.

Here I will illustrate an attractive twelve-point construction which takes as its basis three circles, each related to the other two. The smallest of the three circles is created within the centre of four of the large circles, mutually touching, and the diameter of the middle-sized circle is half the diameter of a square containing the large circle. This gives the diameters of three circles increasing in the ratio of

1 : 1 + 1/√2 : 1 + √2 Development of the grid is shown in the animated graphic above.

This arrangement of circles provides a basis for pattern making with twelve-point geometry when lines are developed joining the intersections of circles, as well as the intersections of horizontal, vertical and diagonal lines linking those points.

Although not a part of the pattern-making here, what is particularly interesting is that the diameters of the circles relate to each other in that they form an arithmetic progression in the ratio of 1 : 1.7071 : 2.4142, to which the next step in the progression – a fourth circle – can be added: 1 + 3 √2/2, making the fuller progression for the diameters of the four circles to be

1 : 1.7071 : 2.4142 : 3.1213, as is illustrated in the larger sketch above.

go to top of page

Thirteen point geometry

The triskaidecagon, or tridecagon, is a difficult shape to deal with when attempting to construct patterns. This is due to the awkward junctions formed with any other regular geometry. Occasionally seen both in nature and in constructed works, they appear to have come about accidentally rather than as the result of a rational process. There is no accurate way to set out a thirteen point pattern in the manner in which most of the other geometries are demonstrated on this page. There are, however, a couple of practical workarounds which might be used if there is the need to construct a diagram which requires a circle to be divided into thirteen parts. Like many other awkward geometrical constructions, in practice this method will use an iterative process to create the necessary divisions. It is based on knowing beforehand the relationship between the radius of a circle, in which will be established a thirteen sided polygon, and the length of each of its thirteen sides.

It is readily understood that, if a circle is divided into thirteen parts about its centre, the angle subtended at the centre by each segment will be 360° / 13, or approximately 27.6923°. If that circle has a radius of 10 units then it will be found that the length of line connecting the points of coincidence of the thirteen radii with the circumference is very nearly 4.8 units.

So, in order to create a circle divided into thirteen parts, draw a circle with radius of ten units and then, using dividers set at 4.8 units, step around the circumference of the circle. An iterative process should refine more precise points along the circumference, but to all intents and purposes, this will be accurate enough for much of the type of work found in traditional naqsh work and may even allow for relatively accurate constructions with timber patterns.

A second way to construct a tridecagon is shown here. Again, it is not accurate, but should create a good approximation.

With its centre on a horizontal line, draw a circle. This will be the circle upon which the approximation of a tridecagon will be drawn. Now, with its centre on the two intersections of circle and horizontal line, draw a second circle of the same diameter. These two circles will intersect in two places.

With its centre on the upper of the intersections of the two circles, draw a third circle of the same diameter. Now draw a line through the same intersection of the first two circles, and extend it in both directions ensuring it intersects with the third circle.

With that intersection as its centre, and the radius set to the lower intersection of the first two circles, describe a large circle. Now measure the distance between the intersection of the first two circles and the intersection of the straight line and large circle. This will establish a measure that will be used to step off distances around the first circle.

With compasses set to this measure and centred at the centre of the first circle, step off intersections with the first circle, each step being centred on the intersection of the previous stepped intersection and circle. Joining these points of intersection will create a good approximation of a tridecagon centred symmetrically about the horizontal line.

go to top of page

The Topkapi scroll

The Topkapi scroll, held in what was the Topkapi Palace but is now the Topkapi Museum in Istanbul, is an illustrated scroll 33 cms wide and 22.5 metres long.

The scroll was prepared around the beginning of the 16th century, probably in Shiraz or Tabriz, Iran and contains an assembly of 114 patterns which appear to be a record of previous designs on the walls and domes of masaajid from between the tenth an the sixteenth centuries.

The patterns have been used by designers as an important resource in the creation of patterns on a number of masaajid, and are of continuing interest to those studying Islamic geometric patterns. While most of the patterns are regular, one of them incorporates a thirteen pointed star, a very unusual construction as 360° can’t be divided neatly by thirteen, a prime number. A simple line drawing of that part of the scroll is shown here; the part of the scroll from which it was taken is shown immediately below.

A complex construction for the pattern has been developed and illustrated in a paper by B. Lynn Bodner, and another view of a tentative construction has been provided by Alan Adams. However, it needs to be understood that a certain amount of distortion is required in order to establish the thirteen points of the tridecagon within the pattern.

A little way below I have set out a slightly different view of the pattern’s construction. It illustrates the pattern overlain by a more accurate distribution of the thirteen points, established geometrically with a drafting programme.

To clarify the design, the animation immediately above has been developed from an illustration in the record of the Topkapi scroll, and shows the star as it appears on the scroll as Catalog Number 30. At a casual glance its significance might be missed. The pattern is that on the right of the two scroll patterns, and the animation shows the hexadecagonal 16 point star top left with the two tridecagonal 13 point stars below and to its right.

However, it appears that the original drawing on the scroll has been wrongly, or carelessly set out in the case of the lower or left of the two tridecagons, even though only half of each is drawn. Close inspection shows that the points on the half of the right tridecagon can be contained by a circumscribing semicircle, though that on the bottom can not.

This error translates to the location of the hexadecagon whose centre needs to be established lower and to the right. This illustration shows where I believe the patterns should be located.

A little way above there are different ways of establishing approximations of a tridecagon. For the sake of this exercise two stars for establishing the tridecagons have been added – without their construction. Then, on the right circle, lines have been drawn connecting every fifth intersection of circle and star line. What is apparent is that the original drawing seems to be significantly inaccurate.

On this illustration, and based initially on an examination of the right tridecagon, the green lines show the correction necessary to establish the pattern more accurately. The junction of the two 45° diagonals will be the meeting point for the stars of the two tridecagons, with their centres aligned along the diagonal from top right to bottom left. From this, a containing square can be drawn which will act as tangents to the two circles containing the tridecagons. The junction of the horizontal and vertical green lines will be the centre of a pattern based on a central hexadecagon. Adding the horizontal and vertical lines from the centres of the red square establishes the centres of the two tridecagons, and their containing circles can now be drawn. The hexadecagon has been added to complete this part pattern on the Topkapi scroll.

go to top of page

Fifteen point geometry

It may seem counter-intuitive that it is not possible to construct a fifteen-sided figure easily. After all, five- and six-point geometries are relatively easy to construct, particularly the latter, requiring no more than a pair of compasses to produce six sub-divisions of a circle. Five-point geometry is also relatively easy to construct and, with it, the setting for golden mean geometry, mentioned below. However, if you combine the two geometries, it is possible to create both 12° and 24° angles, the latter being the internal angle of a circle subtended into fifteen equal parts. The diagram to the right shows the construction of a pentagon in red and, in blue, a hexagon both constructed on the same circle. With a pair of compasses set at the distance between the blue and red lines’ radial intersections with the circle, it is possible to step off fifteen divisions along the circumference of the circle. Incidentally, a fifteen-sided, two-dimensional figure is usually known as a pentadecagon, but you may also see them referred to as a quindecagon or pentakaidecagon.

go to top of page

Seventeen point geometry

On first consideration it may seem impossible to construct a seventeen sided figure with compass and straight edge. However Gauss, in 1796 and at the age of nineteen, proved this not to be the case, and a few years later, Erchinger demonstrated how it might be constructed.

The construction of a seventeen-point figure, or heptadecagon is shown here, which I shall repeat below on this page. My diagrams tend to be over-complex, so I would strongly advise those with an interest in the construction to visit that site which has far more extensive and accurate information both on the heptadecagon as well as dealing with the underlying mathematics of shapes, together with other related matters.

Here, above and to the side, the first sketch is of a heptadecagon, or seventeen-pointed geometrical construction, the circles having been created in the laying out of the points of the heptadecagon on its containing circle. The method of construction establishes two points of the heptadecagon that are its first and fourth points. As there are an irregular number of points on the heptadecagon, compasses set at the distance between points one and four will enable all seventeen points to be established.

The second sketch shows some of the geometry relating to the construction of seventeen point geometry. These are the construction lines created in discovering the position of the fourth point on the circumference of a circle, shown in blue, that is to be developed into the heptadecagon illustrated in the first sketch above.

In order to construct the heptadecagon on the given circle, begin by drawing two diameters at right angles to each other.

On the vertical diameter, AB, locate a point, C, so that AC is a quarter of AB.

Join P1 to C, then locate point D so that ∠ ACD is a quarter of ∠ ACP1.

Locate point E so that ∠ DCE is 45° and, with diameter EP1 construct a semi-circle. This semi-circle will intersect with AB at F.

With radius DF, draw a semi-circle centred on D. Where this intersects with AP1 at G, raise a perpendicular to intersect with the circle at P4.

Now, as described at the beginning of this section, locate the rest of the points along the circumference of the circle by moving compasses around it with radius P1P4. This will create the points in the order shown here in red.

go to top of page

Eighteen point geometry

Eighteen point geometry is obviously related to nine point geometry, a geometry generally considered impossible to set out accurately, but for which there is an approximate construction. However, as illustrated above, it is possible to develop that construction in order to produce a good approximation of an eighteen-sided figure.

The easiest method is to start with the basic nonagon figure and develop the eighteen-point figure by dividing each of the nine internal angles of 40° in half.

In order to simplify the illustrative process here, we start at the point in the construction of the nonagon where the hexagonal petal together with the the curling nonagon figure, both in blue, have been developed.

With compasses set at the same radius as has been used to create the divisions of the nonagon along the circumference of the circle, establish one point at one of the intersections where the hexagon meets the circle – in this case the bottom of the florette – and then describe a series of arcs, each with its centre at the point of intersection of the previous arc and circle.

go to top of page

Nineteen point geometry

The majority of divisions commonly seen are dealt with on these pages and can be seen all around us. Those that are based on simple numbers, or their multiples, are easy to spot, but as larger numbers are reached, patterns based on them are more difficult to construct, and to find. One of the reasons for that is there is not necessarily a reason to make unusual sub-divisions for the very fact that they are not easily recognised. Here, for instance, is a tile which, while not based on an Islamic design, caught my eye and is constructed with nineteen divisions – also known as a nonadecagon or enneadecagon, and a prime number. The basis for sub-division is, therefore, approximately 19° (18.9473684°), an angle that is not possible to construct simply. Note that the pattern is symmetrical neither about its vertical axis or horizontal axis.

While this pattern is not an Islamic one, it is interesting to note that the number 19 has significance not only as a prime number, but also in astronomical calculations. As noted elsewhere, the Islamic calendar is based on lunar cycles and, as a consequence, gives an Islamic year which is around eleven days shorter than a Gregorian year. The Greeks noticed that 19 solar years were almost exactly equal to 235 lunar months, and this information would have been known to the Islamic scholars who came later.

go to top of page

Twenty point geometry

Geometrical patterns created with five and ten divisions are relatively easy to create, and methods for constructing the basic pentagons and decagons are shown in different areas of this page above. It follows that geometry having twenty divisions is also easy to establish – that is by the simple process of dividing each of a ten-point division into two. The two-dimensional, twenty-sided shape derived from this process is termed an icosagon, this illustration shows a circle simply divided into twenty sections. Its purpose is to show something of the loss of clarity when there are this many points on the circumference. At this scale the twenty points of the circumference have not been joined continuously as that would produce lines on the periphery that are little different from the curved circumference itself.

All the construction lines for the pentagons in any of these images have not been shown, but points on the circumference have been joined to produce something resembling an icosagon – essentially those creating the twenty-pointed figure – by the definition of two pentagons and a decagon.

As a general rule, geometric patterns are developed from precise geometric relationships found within the geometry of the originating element of the pattern, this usually being a divisioned circle. In order to begin an exercise for setting out the construction of characteristic stars within the circle it is necessary to select points of intersection within it, and develop the lines of the radiating stars from there.

In this second illustration, above, a development of the first in this note, circles have been constructed at the corners of the two pentagons, their radii being set to that of the side of the pentagons.

These points of intersection are made logically but should be kept to a minimum in order to avoid over-complexity, particularly as these patterns need additional stars linking them to create the familiar patterns with their infinite reach. The lines that are used to create the stars are usually developed parallel with the lines radiating from the centre of the circle, but may also be set at angles when they tend to create a more lively pattern.

In this illustration two of the twenty segments of the isagon have been selected and circles placed marking possible intersections from which patterns may be developed. Seveneen circles are shown here, ten red and seven blue. The red circles mark the intersection of arcs of the circles either with themselves or with straight lines, and the blue circles mark intersections of straight lines. It may be thought that some are unnecessary, or repeated, but they should be understood in the context of their relationship with the central horizontal line as the intention is to develop the lines of the star parallel with it.

The preceding illustration shows how a relatively small number of intersections may be selected with regard to making a decision on where the lines for a star might be most usefully located. But it is evident that there may be many more possibilities, depending upon whether straight or curved lines are considered.

To illustrate the point here, for example, lines have been drawn between all points of the isagon’s circumference to give an indication of the extent of the possible complexity. In order to avoid confusing the number of possibilities even more, none of the curved lines used in constructing the pentagons and decagons are shown here. Close inspection will suggest that there are some intersections better suited for selection than others.

In this illustration – a detail of the full icosagon immediately above – there is a suggestion of how some of the lines of intersection might work better than others. A final selection can only be determined by inspection and experimentation, particularly with regard to expanding the lines of the star outside the icosagon in the construction of linking elements of a geometric pattern.

Here, then, is an animation illustrating a single decision for the location of lines that will define the parallel sides of the arms of a star. The two lines, set one each side of the the lines radiating from the centre, have been extended beyond the periphery of the icosagon, and lines have also been added extending each pair of alternate points on the periphery of the icosagon. The latter extensions create the points of the star within the icosagon, here shown with blue shading as the second phase of the animation.

This shows the area in which the isocagon will be outlined. The third phase illustrates where the an additional ring of decagons will be located in order to begin the process of creating an infinite pattern of icosagons and decagons. The fourth and fifth phases illustrate how the pattern of decagons will appear when completeley surrounding the icosagon. Incidentally, this particular arrangement can not be repeated to create an infinite pattern, but is just here as an investigative exercise.

go to top of page

Twenty-four point geometry

Noticed as an exhibit in London’s Victoria & Albert Museum, this table top is an Italian design from 1805, the design being set out in twenty-four point geometry. However, the table is not shown here as an example of Islamic geometrical design, but because it contrasts with it as a design having the rings of elements established in relation to the centre, not to each other. Apparently, this table top uses one hundred and forty-eight different stone specimens including jasper, agate, porphyry, lapis lazuli, and labradorite.

Twenty-four point geometry is easily set out as it is obviously based on twelve-point geometry, shown above, this design exhibiting concentric rings of pieces of twenty-four, forty-eight and seventy-two elements, with a very non-Islamic twenty-four cartouche-like element border design.

go to top of page

Thirty-six point geometry

Many items in common usage incorporate designs based on simple geometric principles. This saucer, for instance, has its two-dimensional design set out on the basis of thirty-six point geometry, a simple extension of nine- or eighteen-point geometry discussed a little way above. This is a simple but lively design, the sides of the intersecting arches that ring the plate being established from one of the points on the circumference.

While this particular design has not been analysed, there are many ways in which this pattern might have been established. It is likely that one of the methods is shown on this simplistic animation which illustrates one approximation of the design above.

At its simplest, thirty-six radiating lines have been defined from the centre of the circle, each intersecting with the circle’s circumference, and each intersection being used to create the centre for arcs moving through the centre of the circle and intersecting with its circumference. The selection is obviously up to the designer, but four alternative positions for establishing the radii of the arcs are shown here as small, open red circles, the centre for drawing the arcs being the lowest intersection, shown as a small solid red circle. The large red circle is the circle selected to create the thirty-six arcs.

go to top of page

Forty point geometry

The construction of a forty-sided polygon – a tetracontagon or tessacontragon – is relatively simple in that it is based on a ten- or twenty-sided polygon. This illustration omits many of the lines but should be self-explanatory.

With its centre on a horizontal line, describe a circle and, with one of the constructions illustrated above set out twenty lines radiating from its centre. From one of the intersections of the circle and the horizonal line draw a second circle of the same radius. Repeat this for all the intersections of the first circle with the radials. This will establish a pattern of intersecting blue circles, shown faintly here. A line can be drawn from the centre of the first circle through the intersection of any two of these circles – here illustrated by a small red circle – effectively bisecting the 18° angle between each adjacent pair of the twenty radiating lines and creating forty divisions of the circle, each 9°. As can be seen in the last of the animation frames, the forty-sided polygon is difficult to distinguish from a circle, even on the outer, larger circle.

go to top of page

Forty-eight point geometry

Most of the simple constructions on these pages look at the dividing of a circle into a small number of segments. One or two of them tend to be a little more complex – seven, eleven, thirteen, seventeen and so on – but these constructions are usually associated with prime numbers and their solution is to develop them with a certain element of approximation or by trial-and-error.

Occasionally there is a need to develop a circle with a lot of segments. If there are an even number of divisions required it is usually possible to build them with constructions based on four or six point geometries. One such case would be that for a circle with forty-eight segments illustrated in this animated diagram.

With its centre on a horizontal line draw a circle and develop that by constructing six similarly sized circles whose centres are on the circumference of the base circle. Draw a vertical line through the centre of that circle and, from the point where that line cuts the base circle draw another circle thus enabling a diagonal to be drawn through the centre of the base circle. From the point where that diagonal intersects with one of the six surrounding circles, draw six more circles along the circumference of the base circle. The intersections of these twelve surrounding circles will provide the points through which twenty-four lines can be drawn through the centre of the base circle, thus creating forty-eight segments.

While it is not unusual to find geometrical divisions of large numbers used on small scale elements, such as tableware as illustrated with a thirty-six point example a little way above, and following, sometimes the pattern is used deliberately to organise elements other than two-dimensional designs.

In this example of forty-eight divisions – the roof plan of the Lusail stadium in Qatar, one of the stadia constructed for the 2022 FIFA International Football tournament – the geometry governs the elements of the roof’s structure. Although the roof is dished in section, the roof has been designed as a circle on plan. From a structural point of view this is a sensible way of organising repetitive elements into a coherent integral structure. The triangular vocabulary was carried through on the façade of the curved stadium.

go to top of page

Fifty and sixty point geometry

From the same fine dining range of tableware as that shown a little way above come this pair of plates. It is interesting to see that although the plates are of different diameters, an attempt has been made to keep the diamond patterns approximately the same size. In order to do this, the smaller plate has been divided on the basis of fifty point geometry, whereas the larger plate is of sixty point geometry.

However, there is no easy way to divide a circle into fifty equal parts using only a pair of compasses and a straight edge, whether starting from a pentagon or decagon. Nowadays this can be readily accomplished using a computerised drawing programme, or a rough divisioning can be created through trial and error. But it is possible to divide a circle into sixty equal parts with a compass and straight edge, starting from a basis of a pentagon, decagon or, in the construction below, an icosagon or icosahedron – a twenty-sided polygon.

In this diagram, the central red circle has been drawn and then divided into twenty parts by one of the methods illustrated above. For clarity, the lines joining the twenty intersections of the radial lines and circumference of what would be the icosagon have been omitted here.

The faint blue circles have the same diameter as the central red circle and are each centred on an intersection of the twenty radial lines and the central red circle. The centres of the outer two of these red circles are positioned at 126° from the centre of the central red circle, and each intersects with that circle. Red radial lines from the central circle through those intersections divide that segment of the central circle in three. If this is continued round the circumference, a sixty-sided polygon – a hexacontagon – will be created.

go to top of page

Seventy-two point geometry

At its simplest, it is evident that seventy-two point geometry must be related to nine and eighteen point geometry. But, as stated above, its construction is not simply accomplished though can be made by dividing a circle into nine or eighteen divisions by one of the constructions noted above, and then subdividing those angles to create seventy-two divisions.

The graphic above illustrates the geometric division of the circular roof of one of the stadia constructed for the 2022 FIFA International Football tournament in Qatar. That stadium, at al-Lusail, had its roof divided into forty-eight divisions; by contrast this stadium, located at al-Thumama, and also having a circular roof on plan, has had the roof set out on the basis of seventy-two divisions.

go to top of page

The angle of view

Elsewhere on this page there are graphics illustrating the construction and a development of patterns using ten-point geometries which have been used as a starting point to illustrate something of the issues relating to the manner in which we observe patterns. The graphics using the ten-pointed rosette has been simplified here, with the lines outside the rosettes omitted.

Over a very large area the pattern shown above may seem the same as that shown here; in fact, it is very similar, but not quite the same. If you look at the first of the two patterns shown here you will see that the rosettes are stacked on top of each other vertically, forming continuous chains. Each vertical chain is raised or dropped in relation to the adjacent chain in order that a petal of the rosette can make a natural link to a petal in the adjacent two chains. One of the effects of this is to create the effect of pairs of rosettes at 72° to the vertical chains, or 18° to the horizontal.

In the second illustration there are, again, chains of rosettes, but these have been established at 72° to the horizontal in both directions. Note that the residual spaces between the rosettes are exactly the same as in the first example. However, the effect of this new arrangement is to orient all the residual spaces between the rosettes in the same direction. Note that, in the first illustration, these residual spaces are aligned in the same direction in their vertical arrangement, but mirrored horizontally.

Here are the above two patterns again, this time at a different scale in order to give a better understanding of the way in which the patterns differ from each other when viewed over a larger installation. The rosettes are the same size in each graphic, but it is evident that there are two features that create the main differences in the overall pattern, the two graphics being seen to have a different grain or texture when compared with each other.

Firstly, the residual spaces left between the rosettes create a secondary pattern of their own and can be seen to be markedly different in orientation. In this the patterns can be read in the traditional figure-ground arrangement – you can read them both separately, but not at the same time.

The second difference is that, in the upper example, the rosettes can be seen to be established in vertical lines when compared with the lower example where there is a distinct pattern of the chains of rosettes being set diagonally – in fact at 72° to the horizontal in both directions.

However, there is another point to consider, one that has been made elsewhere, but one that should be borne in mind at all times when thinking of patterns. Patterns need to be considered from the point of observation. On pages such as this, we see patterns displayed as readily identifiable two-dimensional patterns. But when viewing patterns on floors and walls we will see them from a variety of angles both vertically and horizontally.

Here are two more versions of the second pattern of the two above. They are the same pattern, but the first is turned through 36° anti-clockwise and the second through a further 36°. Although these are only small illustrations, the change in appearance, the grain of the pattern, is marked.

But those sketch graphics only show the effects obtained when rotating the original pattern within a single plane. If the pattern is viewed with any degree of perspective, either vertically or horizontally, distortion occurs from the single viewing point and creates a different series of textures. The important point to note is that the brain will continue to understand the pattern as being composed of rosettes the same size, despite the distortions of line and size created by the point of viewing and the aerial perspective.

The first illustration here is intended to give a simplified view of the above pattern laid out as a floor covering. Here the eye will automatically read the rosettes in vertical lines as well as in diagonal lines moving both to the left and right. The eye will not read them all at the same time, however, and the pattern will appear mobile as the eye and brain move over it.

The second illustration is intended to be similar to the first in the way in which it is organised, but is meant to show how the pattern might appear when viewed as a covering to a wall surface. Here both the diagonal lines of rosettes are evident as well as the vertical lines. Note in both sketches how the residual spaces are experienced. What can not be shown in these two sketches is the manner in which the perspectives will alter the patterns as the eye moves in relation to them.

Bear in mind that these are both simplistic sketches and are intended only to give a snapshot view in supporting this note. Hopefully they will give you a starting point to consider how grain and structure change with viewing point, and how the brain is trained to receive and interpret the evidence of our eyes.

go to top of page

Using Neusis to trisect an angle

As you can see from the various studies above, it is possible to construct a number of geometrical shapes using just a pair of compasses and an unmarked straight edge. Some geometrical constructions, however, are not similarly possible, though Archimedes is said to have used a system known as neusis to resolve some of the difficulties faced by those attempting to draw what might be thought to be simple geometries. One of Archimedes’ original works, consisting of fifteen propositions, was lost but re-appeared in ‘The Book of Lemmas’, translated into Latin from the ninth century Arabic manuscript of al-Saabi’ Thabit ibn Qurra, in the mid-seventeenth century. A lemma, incidentally, is similar to a theorem, and is a subsidiary proposition that is assumed to be true in order to prove another proposition. There are fifteen propositions in the document, the eighth of them relating to the division of an angle by three. It is possible that this might have been a common method for assisting in laying out certain patterns.

While the theorem holds true, the method of construction does not have the precision of the regular geometries, but is likely to have been accurate enough for craftsmen to use in practice, and is shown here for interest.

The angle to be trisected is ∠ ABC. With centre, B, describe a circle of radius AB. Extend the horizontal line AB. On a ruler mark the same distance as the radius, in this case at points, D and E. Keeping the ruler attached to position C, slide it along until points D and E meet respectively the circle and the horizontal line. At that point, the lines DE and DB – which are both equal – will form an isosceles triangle with the angles ∠ DEB and ∠ DBE a third of angle ∠ ABC. Neusis can also be used in the construction of a regular heptagon, though it is not the method I have illustrated above.

go to top of page

Trisection of a limited range of obtuse angles

Elsewhere I have written about two methods of creating a nonagon, a shape for which there is no accurate method but at least two approximations. One of these methods may also be used to approximate the trisecting an angle of between 90° and 120° – although there is, by extension a method for dealing with angles between 120° and 180°.

The nonagon method is interesting in that it depends on a chord between the two lines describing the angle to be divided in three approximately equal parts.

The nonagon above is the basis for this method. So, rather than go through all that again here, first look at it yourself to gain an understanding of that general method. Essentially, the chord forming a base opposite the angle becomes the base of an equilateral triangle.

With compasses at the point of intersection forming the angle, describe an arc to cut each line at the same distance. Join these two points of intersection to create a triangle.

Now, with the compasses set at the length of the base, describe two arcs, one from each of the ends of the base in order to locate the third corner of an equilateral triangle. From each of those corners describe intersecting arcs in order to drop lines perpendicular to their opposite sides thereby locating the centre of the equilateral triangle. From that centre, describe a circle running through the corners of the triangle.

The next step is to establish the basic nonagon within the circle. This is shown in outline here by the grey patterns for which the construction above should be viewed and followed.

Draw two lines from the centre of the original angle to the points of intersection of the grey nonagon and red circle. The angle has been trisected.

go to top of page

Trisecting a line

While the trisection of an angle requires a marked ruler, as is shown above, trisecting a line is a relatively simple process.

With the centre of a circle located at one end, point A, of the line AB and its radius the length of the line, draw a circle and then draw a second circle with its centre placed at the other end of the line, point B. With the same radius, draw a third circle at one of the points of intersection of the two circles, point C.

Project a line from A through C to intersect the third circle at point D and then draw a line from point D to the intersection of the first two circles at point E. Where the line DE intersects the line AB, at F, that point will divide line AB into AF and FB in the proportions of 2:1. If the latter exercise is repeated by extending the line BC, then the line AB will have been divided into thirds.

go to top of page

Trisecting the side of a hexagon

This illustration has been added even though the method for trisecting the side of a hexagon is not complicated.

Draw a horizontal line and at or near its centre describe a circle. Continue by drawing three circles on each side of the central circle, each with its centre on the intersection of the circle and the horizontal line. This will provide you with a measurement for a large circle whose centre is the same as that of the original circle, and whose diameter is three circles. Draw that large circle.

Using the points of intersection of the small central circle and its immediate neighbouring small circles, project two lines which will be set at 60° to the horizontal line, and which will intersect with the large circle. Connect these points to produce a hexagon. At those points of intersection – the corners of the hexagon – draw circles with the same radius as the original small circle. These circles will trisect the sides of the hexagon.

go to top of page

The Golden mean or section

<

Over time a particular proportion of sides to a rectangle has been found to be attractive to the viewer. This proportion has been named the Golden Section, Golden Rectangle or Golden Mean – Φ – Phi, or its reciprocal – φ – phi.

<

The ratio referred to as the Golden Section is created when two quantities, a and b, have the relationship where

<

a/b is equal to (a+b)/a

<

This diagram, which is based on a diagram on page 73 of a pdf on this site, illustrates the relationship between the Golden Section, Phi, Φ, and its reciprocal, phi, φ, using a right angled Pythagorean triangle with sides in the ratio of 1 : 2 : √5. Accordingly <

Φ will equal (1+√5)/2, or 1·618, and

<

φ, the reciprocal of Φ, will equal (1-√5)/2, or 0.6180.

There are a number of different ways to construct a rectangle with the proportions of the Golden Section. One is to locate side by side two equal squares, drawing their joint diagonal and dropping this down to meet the projected baseline giving an extended rectangle. Add to this rectangle a third square and divide in half the resultant rectangle. The larger of the two vertical rectangles left by cutting the second square with the vertical dividing line has the same proportions as does the rectangle formed by adding that rectangle to the first square.

These can be seen to be related to the Golden Section when the pentagram is combined with the construction of a Golden Section, creating a √5 rectangle which consists of reciprocal golden rectangles.

The proportions of the square to the rectangle are:

1:(√5+1)/2, or 1:1·618.

It is also interesting to see that there is a strong relationship between five point geometry, the Golden Mean or Section and Pythagorean triangles. Here I have shown a basic pentagon coincident with the lines of a Pythagorean triangle of adjacent sides 3 and 4, and hypotenuse, 5. Each of the sides of the pentagon are equal and relate to the extended side in the proportion of 8:5, or 1·618:1. Note that the proportions of 8:5 should not be confused with the measurements of the triangle, 3, 4 and 5.

There are so many aspects of this area of geometry to be discovered in Arabic geometry. This diagram, for instance, illustrates a construction where an eight-pointed star incorporates the proportions of the Golden Section within it, though admittedly not relating to the sides. Here A : B = (A + B) : A, the star being constructed within a grid of eighteen units width and height, the heavier, containing square delimiting a twenty-four unit square which has been the basis for significant investigation on this Ukrainian site.

Bearing the above in mind, here is another interesting construction that creates a line with the proportions of the Golden Mean or Section.

Begin the construction by drawing two lines – one horizontal, one vertical – and which intersect at right angles. With the point of their intersection as its centre, draw a circle of radius x. From the intersection of the circle with the lower end of the vertical line, construct a second horizontal line. This latter line will be that on which a Golden Ratio can be demonstrated.

From one end of the first horizontal or vertical line and their junctions with the circle, set the radius of a pair of compasses to the diameter of the circle – or 2x – and, with the point of the compasses in the centre of the circle, draw an arc which cuts the lower horizontal line. Draw a line from the centre of the circle to this, latter, point of intersection. This will create a triangle with its hypotenuse twice the length of the vertical side of the triangle, and the horizontal side being √3x, or approximately 1.732x.

Draw a second circle with radius 2x and its centre located on the intersection of the first circle with the hypotenuse of the triangle. Draw a line from that centre point to the intersection of the last circle with the lower horizontal line.

The mathematics behind this is not difficult, though I won’t set it out, but the length of this part of the line is (√15)/2 less (√3)/2, or √3/φ. So, A is equivalent to √3 and B to √3/φ – from which it can be readily shown that A : B = (A + B) : A.

There are a number of areas in which the Golden Section can be found to have an importance. A little more has been written about one of these in the Graphics section of this site with respect to the tato, a Japanese form of origami which creates a flat container or purse in which small objects can be held with a degree of safety.

go to top of page

Fibonacci series

I noted above that Fibonacci was familiar with the work of earlier scholars writing in Arabic, but should just like to add a word about the Fibonacci series here. Although the sequence is named after Leonardo Pisano – his father was Guglielmo Bonaccio and he was said to be known as the son of his father, filius bonaccio, hence Fibonacci – its concept originated in the Indian sub-continent over two thousand years ago. The sequence was previously known to Pingala, c. 200 BC, Virahanka, c. 700 AD and Gopala, c. 1135 AD, who both mentioned the sequence explicitly, and also to Hemachandra, c. 1150 AD, the latter discovering the sequence in his studies of poetic meter. Here, its importance is that it relates to the Golden Section in that, if you take the proportion of one number to its neighbour, it approximates the Golden Section – the further along the sequence you go, the more accurate the approximation. This diagram illustrates the way the sequence is built up – 1 + 1 = 2 | 1 + 2 = 3 | 2 + 3 = 5 | 3 + 5 = 8 | 5 + 8 = 13 | 8 + 13 = 21 | 13 + 21 = 34 | 21 + 34 = 55 etc. At its simplest the relationship can be written as:

a : b is as b : a+b

in mathematical terms it is defined by the recurrence relation:

F_n= F_n-1+ F_n-2

The Fibonacci series is now commonly found in the disciplines of mathematics and design, but recently an interesting use of the series has been discovered in the design of a tarsia in Pisa, Italy. Whereas we are more familiar with the lineal development of designs using the series, the tarsia has been constructed with a basis of circles whose diameters correspond to the series from 1 to 55 with additional elements based on half of two adjoining diameters, 44.5 – half of the sum of 34 and 55 – and 17 – half the sum of 13 and 21. A little more about the tarsia has been added in a note on another page.

Related to the Fibonacci series shown above, this graphic illustrates the development of a volute, but in this case, based on the Golden Mean and created on the structure of an isosceles triangle.

Although the basic triangle may be constructed using a pentagon star as shown above, in this case – and for no real reason other than to demonstrate an alternative process – the construction began with the drawing of a rectangle in the proportions of the Golden Section. The construction of the rectangle is not shown here as it was measured for simplicity. The top of the triangle was then discovered by rotating the two top corners of the rectangle inwards around the lower corners of the rectangle.

The isosceles triangle formed has, therefore, two sides which bear their relationships with the base in the proportions of 1.618:1. One long side of the triangle is then divided into the same proportions by describing a circle centred on the lower left corner and radius the right corner, the circle dividing the right side of the triangle. This first point of division establishes the centre for the first section of the volute. The process can then be continued, steadily diminishing and creating, in this case, a volute of seven sections.

Note that the curve does not have a continuing diminishing radius as each segment has a specific radius. The consequence of this is that there is a noticeable flattening of the curve at the corners of the triangles, there being no mutually coincident tangent located at this change in direction of the segments that make up the curve. Compare this with the volute that follows where the contiguous tangents meet, not at 72° as in this case, but at right angles, creating a more naturally curved volute…

Another illustration using the properties of Fibonacci proportions can be seen in this graphic. On a horizontal line a small circle has been constructed, the lowest point of its circumference forming a tangent with the horizontal line. A vertical line is raised through this junction and a point determined on that line, its distance a diameter of the small circle from its centre. From that point, two lines are drawn touching the small circle as tangents, intersecting with the horizontal line to create an isosceles triangle.

A circle with its diameter twice that of the small circle is drawn, its centre coincident with the centre of the small circle and passing through the corners of the isosceles triangle. With its centre on one of the corners of the triangle a circle of the same diameter is drawn to meet the first large circle and five more circles are constructed on the first circle, their centres on the intersection of the first two large circles. This is the standard construction for a hexagon.

From the intersections of the second, fourth and sixth large circles with the internal small circle, lines are drawn to the three corners of the triangle, their intersections creating a smaller isosceles triangle. The two portions of the line shown on the illustration are in the proportions of the Fibonacci series, as is the ratio of the two triangles.

While I’m at it, and I know this has little to do with Arabic geometry, I thought it might be useful to place here a reminder that these geometries were used in other parts of the world. To the side is a detail of the volute on a nineteenth century Ionic capital, developed from those which preceded it over two thousand years previously. They were developed with a strict geometry related to the understanding of natural forms at the time. Although similar to the geometry shown above, this particular example is not based on a Fibonacci series.

Later, these constructions were developed, again based on similar geometric principles. This sketch illustrates the basis on which a volute may be formed. What is significant is that although the volute looks as if it is a constant curve, it is not: it is a series of joined quadrants. Quadrants are formed of increasing size, each linked to its preceding quadrant with its centre further offset. I have drawn each quadrant a different colour to illustrate the sequence, though it can be readily imagined how variations can be established to produce the lines of the volute closer or further apart. Incidentally, the word ‘volute’ is derived from the Latin word for a scroll.

In order to clarify the above construction, here is the method I used. Create a square and extend its sides unidirectionally on one side only. Within the square construct a circle. With compass at position ‘b’ draw an arc anticlockwise from position ‘a’ to meet the vertically extended line from the square. With compass at point ‘c’ extend the arc anticlockwise to the horizontally extended line. From point ‘d’ extend the arc to the horizontally extended line. From point ‘f’ extend the arc to the vertically extended line. From point ‘c’…etc.

Although this construction is often used to produce spirals or volutes, the accretion of quadrants does not produce an accurate mathematical description of a spiral. A spiral is described by a line that increases its distance from a point by a constant factor as it moves around that point on a plane. That particular spiral, illustrated above, is a logarithmic spiral, and not an Archimedean spiral, illustrated here, which is distinguished by its lines being set parallel to each other, rather than increasing in distance as does the logarithmic spiral.

You can see in the above diagram of the logarithmic spiral, one of the many forms commonly to be discovered in the natural world. Shells, fruit and flowers are often found with this type of geometry driving the arrangement of their forms, the patterns being exhibited in a number of ways, all relating to their growth structures sometimes in their external form, often in cross-sections made across them.

Both the pineapple to the right, as well as the pine cone below it, have grown with eight divisions spiraling clockwise and thirteen anti-clockwise. These numbers, of course, are both in accord with the Fibonacci series and seem to be one of the most commonly found bases for the growth of plants – 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 etc.

Yet while arrangements based on eight and thirteen divisions seem to be the most commonly discovered in nature, those based on thirteen and twenty-one divisions seem also to be found everywhere you look. In this yellow flower head, for instance, it can clearly be seen that there are thirteen spirals rotating in an anti-clockwise direction, and twenty-one clockwise. There is a design coherence in the movement created in this static arrangement that contributes greatly to their attraction.

I should add that similar forms are used in the creation of designs expressed in work such as architecture and painting, and have been for thousands of years, the designers taking their geometrical structures from those which they have witnessed in the natural world around them. Designers have taken their lessons from nature and have attempted to develop their observations into a codified series of proportions which, they have argued, may improve our relationship, resonance or psychological comfort with the product of their designs, particularly architecture.

This has led to a number of proportions suggested as being suitable if not necessary for the basis of design work, perhaps the two best known being Leonardo da Vinci’s ‘Vitruvian Man’ and Le Corbusier’s modular systems which he utilised in the design of his buildings.

There is a mention above of an Archimedian spiral, noting that, contrasting with the construction of a logarithmic spiral, the spiral was characterised by having the distance between each loop of the spiral a constant. But there are two other spirals which should be mentioned as it is important to note their differences – the Bernoulli or logarithmic spiral and the Fermat or parabolic spiral, although the latter is a type of Archimedian spiral.

Note how the lower illustration – which has been derived from the lineal graphic above it by the addition of dots at regular intervals along the curves – bears similarities to the centre of the flower illustrated a little way above, a common pattern found in nature.

The general formula for Fermat’s spiral is given by:

r²=a²θ.

where ris the radius, ais a real number, and θthe angle from the x-axis.

This can be compared with the setting out of an Archimedian spiral:

r=a+bθ

where ris the radius, aand bare real numbers – acontrolling the turning of the spiral and bthe distance between successive turnings – and θthe angle.

The formula for a logarithmic or Bernoulli spiral is:

r=ae^bθ

where ris the distance from the origin, aand bare real numbers, and θthe angle from the x-axis.

But returning to the Fibonacci series, this may also be seen in the external surface of the pineapple above which has eight spirals in one direction and thirteen in the other; and the same is true for the pine cone in the photograph below it, underneath which is an immature pine cone on which you can also see the spirals. Incidentally, sunflower heads have thirty-four florets spiralling in one direction and fifty-five in the other direction, continuing the Fibonacci series. The lowest of these four photographs, of a cactus, while not based on a spiral configuration, shows it has a geometry based on thirty-four, again one of the numbers of the Fibonacci sequence.

There are many plants and other aspects of nature which exhibit this form of spiralling geometry. Here to the right is a dahlia, though I have to admit I’m not sure of the numbers involved due to the lack of accuracy of positioning in the petals of this lovely flower. I think it is thirteen and eight but, as I say, I’m not sure. However, you should be able to see the resemblance with the geometries of the pine cone and pineapple above. Geometry, whether it is as obvious as three-point, four-point and so on, or is related to Fibonacci proportions as these plants are, produces a seemingly endless variety of effects. Below the dahlia is a photograph I took of a cactus. Although you may not be able to see it easily, there are twenty-one spirals in each direction, again a number associated with the Fibonacci series.

Wherever you look there are patterns to explore. I have not meant this parts of my notes to be a series of photographs of spirals and designs associated with the Fibonacci series or other groupings, but I think it is useful to look at these for a minute to get an idea of how prevalent this is. Whether there is an identifiable pattern or whether it is a regular progression there is considerable difference in similar geometries though, of course, these all have a three-dimensional aspect and I am really only dealing with two-dimensional geometry here.

Before I end this note I would just like to add three more images as they are common examples, should be well known to most people, and are striking examples of this form of natural geometry.

The first two photographs are of marine shells, the first showing a cross section of the shell of a nautilus pompiliuswhere an approximation of a logarithmic spiral governs the growth pattern of the buoyancy chambers the cephalopod uses in order to maintain its buoyancy in the water.

Found on a beach in Qatar, I don’t know what type of shell this is, but this second photograph is of one that has been ground away by the action of the scouring of sea water and sea bed aggregates leaving the spiral form of its construction clearly exposed.

The third photograph is of a South African polyphylla aloewhich shows the almost perfect geometry of its spiral form with the leaves increasing in size as they move towards the outside of the plant. There will be a mathematical relationship governing this growth, though I am not able to say what it is. It is not formed in the same manner as lies behind the carpet below, but you should be able to see an interesting similarity.

I have added this photograph as it demonstrates what is to me an interesting point. This Persian carpet has been constructed with what appears to be a Fibonacci geometry driving the pattern. But there are thirty-two spirals, not the thirty-four you might anticipate from Fibonacci. So the design is based on four- or eight-point geometry from which the spirals are derived.

Here I have attempted to draw what I believe to be the geometrical construction behind the pattern. The inaccuracies are likely to be a combination of the angle at which I took the photograph, possible inaccuracies in the construction of the carpet and my inability to work out the exact points of geometrical derivation. However, I think it’s close enough to see the likely basis. Note that I have not shown the thirty-two divisional – or 11¼° construction – as they are just sub-divisions of 45° and would complicate the diagram.

The reason for briefly describing these geometries is to show that some of them are relatively complex, and that we tend to take them for granted. Despite this, it is instructive to watch craftsmen on both sides of the Gulf using these geometries with only a straight edge and string to construct complex patterns.

Many of these are undoubtedly traditional and easily learned but, from observation, changes and customisation still takes place, making each element of work unique while informed by and related to the country's heritage.

Having said that, it is undoubtedly true that the geometries used and patterns formed in Gulf design, particularly naqsh, are relatively simple. Naqsh is, after all, a relatively simple material, the setting out and carving traditionally carried out with drying juss mortar where speed is imperative. It is relatively easy to carve dry although, wet or dry, it is a relatively crude technique.

However, the designs produced and techniques used in this relatively simple craft differ along the Gulf. More sophisticated designs are found further south, the patterns there being more fluid and the elements of the design finer.

go to top of page

Other systems of proportion

Further up the page I have noted briefly systems of proportions, particularly relating to the Golden Section, the Fibonacci series and Vitruvian man. Here, although it may seem as if it has little or nothing to do with Arabic geometry, I should note other systems of proportions as they have also been used in the design of buildings. The best known of these is, perhaps, the system developed by the Swiss architect, Le Corbusier, a system he termed ‘Le Modulor’, and which he based on the Golden Section.

more to be written…

go to top of page

Relationship of Arabic calligraphy to geometry

Although I don't want to deal with calligraphy here in any detail, it is relevant to note that Arabic calligraphy is firmly based on geometric proportions. For those who would like to learn more they might look at this beautiful and scholarly work.

At its simplest, the most important form is that illustrated below and shows, on the right, the first letter of the Arabic alphabet, alif, which equates to the long 'a' in English. Note that it's proportions are 1:7. The style is known as al khatt al mansub and was designed by the great Abbasid poet and calligrapher, Abu Ali ibn Muqlah, who died in Baghdad in 940. To the left of the alif is the letter 'ain which shows a cursive letter in the alphabet based on the same size dot. While some believe he invented a particular calligraphic script, it is more likely that he was responsible for codifying existing scripts in accordance with a series of geometric principles based on rhombus created by the pen’s nib, as illustrated above.

Finally, there are two points which should be borne in mind with regard to calligraphy and its relationship with rigid geometry:

• there are a wide variety of manuscripts in Arabic, and the alif can differ in its proportions from 1:3 to 1:12, and
• traditionally, letters are formed with a pen which, while being held at an angle, is also varied by the scribe as he writes to create angles other than the basic 45°.

more to be written…

go to top of page

Design and ‘e’

While it may be thought to have little or nothing to do with geometry, I should also mention here the relevance of the mathematical constant ‘e’. I hope to expand on this relevance later. Generally known as the base of natural logarithm, ‘e’has a significant importance in mathematics, as great as that of pi. ‘e’is an irrational number which, to compare with other numbers given on this page, can be taken as 2.718 to three decimal places. You might note the following square roots:

• √5 = 2.236
• √6 = 2.449
• √7 = 2.646
• √8 = 2.828

You can see that ‘e’fits between √7 and √8, though has a very different mathematical significance. I have placed these numbers here as the theory noted in the above paragraph has a theoretically wide possible variation; with ‘e’being valued from two to seven, in fact.

The reason I have introduced ‘e’on this page is that it is held to be a factor relating scales of elements within an overall design. It is argued that a design may have significant internal coherence when its elements have that relationship at different scales. Moreover it is held that this relationship also applies to the structure of biological forms. The paper referred to here is argued on the basis of the design of traditional carpets but, by its very nature, there should be no reason why these relationships might not hold good for other areas of design. In fact, in another paper this is explicitly stated, relating the comments to the work of Christopher Alexander, who based his work on the study of carpets but extrapolated the concept to design in general.

Its relevance on this page is in an aspect of Islamic design alluded to on both this page as well as others in this section of the site: the complexity in apparent simplicity that is so often a characteristic of geometrically based Islamic design. Above I have perhaps concentrated on the complexity achieved from simple geometries, but here I wish to introduce another way in which designs might be seen.

more to be written…

go to top of page

Application of traditional patterns

In Qatar, traditional patterns are only applied in four areas:

• naqsh panels,
• carved timbers, particularly the enf door posts,
• woven patterning in the rush ceilings, and
• painted patterns on boarded ceilings.

None of these patterns has developed to the extent seen in the repetitive patterns of Persian tilework. While the patterns found in the Gulf are non-figurative geometrical designs, they have not developed along with the mathematical complexity seen in Persia, north Africa or Andalusian Spain.

go to top of page

Platonic solids

Towards the top of the page I mentioned briefly the related concepts of sacred geometry and geomancy. That geometry was essentially two-dimensional, but there are three-dimensional forms too, of course. Of these there are basically only five regular three-dimensional forms, the group being known collectively as the Platonic solids after the Greek philosopher and mathematician, Plato, who wrote extensively about them in his philosophical studies. My purpose in mentioning them here is only to introduce them as a development of two-dimensional geometry. Anybody wanting more information about them should look elsewhere.

Despite this naming, they are generally considered to have been discovered by Pythagoras or his group, though it is possible that Theaetetus, a contemporary of Plato, may have been responsible for the octahedron and icosahedron. While their discovery and naming is credited with Pythagoras and Plato, a point to bear in mind is that, like much else, there is considerable evidence that they were discovered centuries earlier in other parts of the world.

The five forms are known – in ascending order based on the number of sides – as a:

• tetrahedron,
• hexahedron,
• octahedron,
• dodecahedron, and
• icosahedron

These three-dimensional forms are considered to be the bases of all natural forms and, as such, are related to the very essence of the universe.

The five figures are composed as follows:

• the tetrahedron has four equilateral triangular faces and six edges,
• the hexahedron six square faces and twelve edges,
• the octahedron eight equilateral triangular faces and twelve edges,
• the dodecahedron twelve equilateral pentagons and thirty edges, and
• the icosahedron twenty equilateral triangles and thirty edges.

These forms might be considered while thinking of the two-dimensional geometries as well as the patterns derived from them. Two-dimensional geometries are often developed into either a three- or pseudo three-dimensional geometry by the use of shadow patterns or inter-weaving. My own experience, when working on or contemplating two-dimensional patterns, is that it is relatively easy to move into a third dimension view as the patterns form and re-form in front of you.

go to top of page

Seventeen different patterns

This note and the accompanying diagrams follow on from a note made on the following page, entitled symmetry. Its mention there has more to do with its meaning relating to balance and design aesthetics. But in the area of patterns, it has a more complex meaning, one to do with the way in which symmetrical patterns are produced and categorised, a complexity governed by the mathematics of group theory. The notation used in the accompanying illustrations is the IUC notation adopted by the International Union of Crystallography in 1952. Incidentally, you may come across other systems of notation such as the orbifold notation of John Horton Conway. This is based not on crystallography, as is the IUC system, but on topology.

Although there may appear to be an infinite number of patterns to be seen in the world around us, in reality there are only seventeen different ways in which patterns can be repeated two-dimensionally. This is sometimes referred to as ‘wallpaper’ patterning and commonly describes patterns created as covering on walls, floors and ceilings.

Examples of all or nearly all of these patterns can be found in the Alhambra, Spain. It has been stated by Grünbaum that there are four patterns missing from the Alhambra – pg, pgg, p2 and p3m1 – though the latter two have been found to have been constructed coaevally in Toledo. He also stated that the former two – pg and pgg – are not found in Islamic art at all, though this has been disputed. As you will see in the first sentence of this paragraph, there is even dispute about the number of symmetries found in the Alhambra. It is not my intent to set out the arguments for and against here; those who might have an interest in this issue should look elsewhere.

There are certainly a fewer number of designs than this to be found in the Gulf, if for no other reason than there are not that many examples to analyse and, of these examples, few cover areas of the size required to see the repeats effectively. More than this, the patterns seen in Qatar tend to be iconic and are not designed specifically to cover large areas as might be found in, for instance, the glazed tilework on many buildings in Iran and further afield in the Indian sub-continent, Egypt and Morocco among others. Tiling, of course, lends itself to mass production, the tiles enabling the formation of a wide variety of different arrangements and patterns.

It is possible that, if there had been a tradition in Qatar of tiling, there might have been a very different situation as craftsmen from Iran would most likely have made their influence apparent. But the fact is that the materials from which the architecture and its detailing were constructed in Qatar were relatively soft. Patterns were confined mainly to doors and wall panels, both of relatively transient materials, particularly the juss from which wall panels and patterns were constructed. The character of the juss, with its need to work relatively quickly, led to few of the patterns on the walls of Qatari buildings incorporating symmetrical geometries. Having said that, it is perhaps more accurate to state that where symmetrical geometries were employed, they were relatively simple.

There are two final points I should make. In writing about the seventeen different forms of symmetry, I should emphasise that this relates to a single colour and to flat patterns.

In the many examples of patterns to be found both in Islamic and other art, colour is often a major element of the design. If you include permutations of two colours, there are a possibility of an additional forty-six symmetries that may be found.

There are also complexities brought about when the patterns are not flat. A number of designs are enlivened by their designers by creating the appearance of three-dimensional work by simulating lines running over and under each other. Generally this will break the possibility of simple reflectional symmetry.

more to be written…

go to top of page

Four basic pattern types of symmetry

The seventeen different ways for patterns to be formed, and illustrated in the five diagrams located above, have been established mathematically but in the diagrams are described notationally. Symmetry, in this sense, is created with the movement of a shape by one of four methods that preserve the relationships of distance, size, angles and shape. Each basic pattern type is constructed by taking an element and then repeating it by

• rotation, which turns a shape around a fixed point,
• translation, which simply moves a shape a specific distance without rotating or reflecting it, and
• reflection, which mirrors a shape across a fixed line.

In addition to the three types above, there is a fourth type,

• glide reflection, which reflects a shape across a fixed line, but then translates or moves it in a direction parallel with the line of reflection. It is the only type of the four that is established in two movements.

There are many sources of information for those interested in learning something of the mathematics governing the patterns. One useful reference is this which gives a simple view of the alternatives. These five groups relate to the diagram at the head of this section, just above:

• the first group of four are made without rotation and are known as: p1, pm, pg and cm,
• the second group are constructed using rotations of 180°, without rotations of 60° or 90°: p2, pgg, pmm, cmm and pmg,
• the third group are constructed with rotations of 90°: p4, p4g and p4m,
• the fourth group use rotations of 120°: p3, p3ml and p3lm, and
• the fifth group are constructed with rotations of 60°: p6 and p6m.

The coding system that I have used here is that of the International union of Crystallography, but alternative systems have been developed, such as those relating to topology, and other classifications have been put forward. I have not yet found a simple way to describe this to the layman other than this Open University programme.

With these basic arrangements there is an infinite number of ways in which patterns can be arranged together to give different effects. Shape, colour and texture are all used in Arabic design, as is the effect of three-dimensions in more sophisticated work.

go to top of page

Determining a pattern type

This diagram relies on information from two different sources, although there is a third and larger version of it here where there is also more to be read on the subject of seventeen patterns. Reading the relevant sections of the sources should give a far wider understanding of the subject, though it is fair to say that elsewhere there is a considerable amount of literature dealing with the mathematics behind wallpaper patterns. This is a specialised area of mathematics but one that might be investigated further with benefit.

The diagram sets out a method for determining the category into which a particular symmetrical pattern might fall. The four categories of pattern illustrated in the diagram above –

• translation,
• reflection,
• rotation and
• glide reflection

– govern the process that starts with the number of rotations there might be, ranging in order from none to six – 0, 2, 3, 4 and 6. The orders relate to the number of rotations that can occur within 360°.

• Order 2 – 180°
• Order 3 – 120°
• Order 4 –   90°
• Order 6 –   60°

Starting with the rectangle on the left marked ‘Smallest rotation’, follow the line that defines the smallest number of rotations to be found in the pattern. The questions asked relate to whether or not there is reflection, rotation or glide reflection with regard to mirror lines or axes. The selection based on the decision or decisions will lead to the appropriate definition of the pattern type. I hope that’s clear…

go to top of page

An eighteenth geometry

Before I finish with these basic notes on Islamic geometry, I should mention that there is one other set of patterns to add to the seventeen I noted above as being the total number of basic patterns. This eighteenth pattern may or may not be found in Islamic designs, but is notable for the character of its non-repeating pattern. It was discovered in 1974 and subsequently patented by the mathematician, Dr. Roger Penrose.

What is unusual is that previously it was thought that only patterns based on two, three, four and six rotational symmetries could tile a plain surface, and that five- and ten-sided geometries could not.

An interesting effect is created when running the eye over the basic geometry as the eye automatically finds familiar shapes which disappear as different shapes take over. This happens with the eye finding both two-dimensional shapes as well as three-dimensional shapes as the brain suggests three-dimensional shapes with which it is familiar.

Relying on two rhombi using angles based on π√2 – 36°, the basic angle of the Golden Section – the patterns are assembled according to a set of rules he devised to ensure no repetition.

The two rhombi are assembled into patterns using their two characteristics illustrated here. The rules require that:

• two adjacent vertices must be of the same colour, and
• two adjacent edges must have both arrows in the same alignment, or no arrows at all.

These basic two elements – in accordance with their assembling rules, can be grouped into eight permissible clusters. From these, non-repeating patterns can be constructed giving, in theory, an infinite and non-repeating design.

It is interesting to speculate on how this patterning would have been used by Arab designers had the basic geometry been discovered a thousand or so years ago. My feeling is that the asymmetry would be admirably suited to the premise of man’s inability to know everything, and the infinity demonstrable in two dimensional design. It would have been an ideal way in which to cover plain areas of walls in a non-repeating pattern.

Prior to this, in 1974, Penrose established the basic units that first created what came to be known as Penrose patterns or tilings. The two shapes were nicknamed darts and kites and were derived from a pentagon as is shown on the left diagram of these illustrations.

The dart is produced by adding two of the central triangles together, and the kite by the addition of the two side triangles. When used to form a Penrose tiling, with the increase in the numbers used in the pattern, the ratio of kites to darts approaches the Golden Section, φ or 1.618. Note in this lower illustration, that the dart and kite shapes, when added together, form the rhombi that are sketched just above. These are known as Penrose rhombs.

go to top of page

An aperiodic monotile

For many years mathematicians attempted to find the lowest number of tiles which might be formed into a non-repeating two-dimensional pattern.

From over twenty thousand this number was reduced by Robert Burger to 104 and then by Donald Knuth to 92. In 1969 Raphael Robinson got the number down to six then, in 1974, Robert Penrose found it to be possible with only two tiles and for some time this was accepted as the lowest possible number for this character of pattern.

However, in March 2023 an important announcement was made; a single aperiodic tile was discovered with which it would be possible to completely tile a two-dimensional space. The polykite the authors refer to as ‘the hat’ is shown in this illustration in which the underlying geometry of a subdivided hexagonal grid can be seen.

The mathematics behind this pattern is far too complex to be dealt with here, so for more information on this pattern, please see this document.

go to top of page

Decagonal and quasi-crystalline tiling

Having written the above note on Penrose some time ago there has been, in February 2007, a significant paper written on the possibility that medieval Islamic artisans produced their geometries with the aid of girih tiles. These tiles are equilateral polygons decorated with straplines which, it is argued, permitted the creation of complex periodic patterns. The tiles were of five shapes: hexagon, bow tie, rhombus, pentagon and decagon.

It is interesting to read the comments made on the paper where there is doubt on the authors’ argument that Islamic artisans truly understood the meaning of quasi-crystals, rather that ‘the variety of the geometric tesselations covering the wall of Moorish buildings appears to be more consistent with the search for extra vistas of beauty, rather than inspired by a sudden mathematical discovery’. Another comment also notes that periodic patterns, including the use of all seventeen plane groups, can be traced back much further back in time, to ancient Egyptian ornamentation…

Commentary also includes mention of the Vedic square in pattern making; however, for the purposes of this note, here is an illustration of the five tiles:

Termed ‘quasi-crystalline’ patterns, they are two-dimensional shapes which fill all of a space, but without the translational symmetry characteristic of true crystals. Essentially this means that attempting to match an exact copy of the pattern over itself will never produce a precise match. In this they are similar to the tiles to which Dr. Penrose put his name in the 1970s. The thesis is that Islamic designers developed these geometries between the thirteenth and sixteenth centuries, and that the geometries were not familiar to Western mathematicians for a further five hundred years. Whether this development is accidental or not is debatable.

The five tiles can be seen in the graphic above and comprise:

• a regular decagon with ten interior angles each of 144°,
• a lozenge or elongated hexagon with interior angles of 72° and 144°,
• a bow-tie with interior angles of 72° and 216°,
• a rhombus with interior angles of 72° and 108°, and
• a regular pentagon with five interior angles each of 108°.

The sides of the different shapes are all of the same length, and their internal angles multiples of 36°. The strap lines which decorate the tiles continue across the junctions of tiles to produce the continuous patterns typical of these tiles.

Here are the same five tiles set against their ten-point constructional geometry.

The illustrations of the five basic tiles include their concomitant strapwork lines. Although it may seem a little complex, I have actually had to omit some of the construction lines for clarity. But it is the construction lines that are most associated with the patterning construction of Islamic design and for which the geometries I have described above form the basis. Using these five tiles as templates, it is argued that it would not have been difficult for artisans to assemble the complex patterns that we associate with Islamic design. In fact it is argued that this might be a far simpler method than organising the more complex strapwork geometries and tiling or decorating within them. Having spent a long time working on this kind of geometry I have to say I have a feeling that this might well be the case.

If it were the case – that Islamic artisans designed and used these tiles – then it explains how they were able to accomplish the complex setting out of their designs without making the mistakes that would have been likely if they had to create each line segment separately. It is not thought that they assembled the tiles individually, but that it is more probably that the five tiles were used as templates to trace patterns for fixing mosaics.

At present this thesis is unproved but, as I have written elsewhere, considerable advances were made in the Islamic world in science and the arts, based on earlier Greek and other work. Little of this has been taught in Western schools and universities as evolving from Islamic study and it seems there is yet more research to be carried out.

go to top of page

Long-range order of quasi-periodic patterns

Since the work of work of Lu and Steinhardt was published, more interest has developed, especially with the establishing of a model illustrating a global multi-level hierarchical framework. The model makes it possible not only to describe long-range translational and orientational orders of quasi-periodic formations in Islamic design, but to grow infinite formations of quasi-periodic patterns, including the Penrose tilings noted above. Its importance lies not only in its thesis governing infinite patterns, but that this knowledge would have been known to Islamic designers hundreds of years ago.

This first graphic illustrates a regular decagonal grid that can be developed into a series of nested decagons that might form the basis for an Islamic pattern through infinite expanding or diminishing – as shown here – repetition.

In common with traditional Islamic patterns constructed with compass and straight edge, this work develops its geometry from a central point, one that Critchlow refers to as having both a metaphysical and a physical presence. He develops the argument that Islamic patterns are established with star units positioned in relation to basic grids, the grids defining the type of symmetry and the stars the internal pattern designs. The inference is that it is the underlying grids that must resolve the order of Islamic quasi-periodic patterns.

Elsewhere I have illustrated how a pentagon and decagon may be constructed, as well as one of the ways in which patterns may be developed from the decagon. Here there is a description of how the setting out of quasi-periodic patterns may be established, based on the paper describing long-range translational and orientational orders of quasi-periodic formations in Islamic design. The paper should be explored for a more detailed explanation than is given here.

The basic decagon, illustrated above, can form the basis for a two-dimensional grid, and may also be used to generate patterns within it. For instance, in these three graphics, the grid underlying the pattern has been created by drawing lines between, from left to right, every second, third and fourth corners of the decagon, with a simple star created over those guidelines.

This next group of three patterns were constructed by drawing additional guide lines within the decagon, joining together points of intersection of the original guidelines. The first of the three patterns can be seen to have a different character from the second and third patterns, both of which are characterised by a radiating lozenge motif.

The first of these patterns is the same as the central pattern in the three patterns above. All three of these patterns are related in that that they are based on the same guidelines. The first two are very similar, the difference between them being the manner in which the centre is treated. The third pattern can be seen to have more similarities with the pattern on the left, immediately above.

The main point to make with demonstrating these eight patterns is that they are all simple variations based on the joining of intersecting guidelines of the decagon. By inspection it is easy to see that other patterns might be drawn from the same basis and, if other guidelines are developed, even more patterns might be evolved. All of this would have been easily managed with compasses and a straight edge.

By extension, there are similarly a number of different ways in which linked decagons may be joined in order to give a natural flow to the continuous pattern they produce. Unlike hexagons, which fit naturally together, decagons will always have residual spaces between some of them when they are joined together. In this sketch, two arrangements for joining the basic decagons are shown; the one on the left with five linked decagons and that on the right with seven. Note that, in the five linked decagons, the residual shape in the centre is mirrored vertically in those that will link to the next groups of five decagons.

Also note that if each of the decagons is rotated through 18°, a different overall pattern is obtained with different linkages between the decagons. Also, note that the size of each of the decagonal rosettes is slightly smaller in this second sketch as their corners stretch from the midpoint of each face of the underlying decagon compared with those above which stretch to its corners.

This sketch illustrates one of the simplest ways in which the space between five linked decagons might be organised in order to provide natural linkages between the pattern lines within the decagons. The guide lines, here shown white, are a combination of extensions of pattern lines within the decagons and lines linking the centres of the sides of decagons.

The sketch immediately above shows a linkage pattern between the decagons that is symmetrical with respect to each of the five decagons that surround the residual space. Here it is not. Symmetry is realised only mirrored around a vertical line passing through the centre of the pentagonal residual space. This creates, in the centre of the pentagon, a more complex shape than usual.

Here the linking pattern in the centre of the pentagon is, like the first, symmetrical with respect to the five surrounding decagons. However, it is more complicated to set out. The guidelines linking the corners of the surrounding decagons with the corners of the internal decagonal star are not extensions of the lines forming the surrounding decagonal stars, though they may at first appear to be; they are slightly cranked. The guidelines are created by first extending the sides of the surrounding decagons so that, extended, they form a smaller central decagon, shown in white. From the central points of the sides of this central decagon, the central decagonal star can be constructed and, from the same central points on the guiding decagon, lines can be taken back to meet each of the surrounding decagons.

Compared with the linking of five decagons, the linking of seven decagons is relatively simple as there are fewer alternatives available to the designer. This sketch illustrates the most obvious lines with the continuation of lines from two of the decagons. It would be possible to make alternative selections, but they would not create as natural a pattern as is shown here. Rotating the seven decagons individually by 18° creates no benefit either, in fact the patterns formed are less obvious and appear more unnatural.

This lower illustration shows in the top of the left example, the simple design solution indicated in the sketch above. That below it is possible, but not as elegant. The top of the two examples on the right – these decagons being rotated 18° compared with those on the left – is a logical solution, but creates a diamond shape that is small when compared with the sizes of the shapes produced in the rest of the decagons. The lower example is not an attractive compared with the other three.

more to be written…

go to top of page

Tessellations

Tessellation refers to the complete covering of Euclidean plane surfaces with tiles such that there are neither gaps between the tiles, nor do they overlap. The term takes its name from the Latin word, tesserae, given to the pieces of hard materials used to create, usually, mosaic pavements, though it is possible to see tessellation in many other design applications. Tessellation is sometimes alternatively referred to as tiling.

There is considerable information on tessellations elsewhere and it is not my intention to attempt to cover it. The notes here are an introduction, a simplistic view of tessellation as it might relate to the areas of Islamic geometry noted on these pages.

Much of the notes written on these pages deal with the geometry of work that has been carried out in glazed tilework or in wooden elements established as panels on doors or walls. Generally the geometry is two dimensional with, in a few cases, elements of the pattern raised to produce a more legible design. In both cases the designs follow lines selected from the underlying geometrical pattern, a geometry that can be quite complex and is likely to produce elements of different sizes and shapes. While tessellation may be created of a number of elements in different shapes and sizes, much of it appears to be concerned with the repetition of similar units. It has a particular relevance when seen in relation to the seventeen translational geometry patterns discussed above, sometimes referred to as ’wallpaper‘ patterns.

It should be borne in mind that tessellations generally can be experienced, or thought of, as continuous, infinite patterns of which only a part is being experienced by the viewer.

Not all regular shapes can be tessellated to cover a plane surface. Some shapes will require the addition of filling pieces in order to create a complete covering. Shapes with three, four, five and six sides are the only regular shapes that will tessellate by themselves and the hexagon is, of course, comprised of six triangles. All triangles, all quadrilaterals and three types of hexagon will tessellate. No convex polygon of over six sides will tessellate. But even with these simple shapes it can be seen that only the square can be slid vertically or horizontally in order to tessellate; the triangle and hexagon must be rotated or ‘glided’ in order to produce complete coverage and, with these latter three shapes, there will be an irregular edge condition where the tessellation is not infinite.

The illustration of tessellations above includes a five-sided shape which will be discussed below, but generally tessellations are considered to be capable of including only three, four and six sided regular shapes. The argument is that in order to rotate polygons around a single point, the internal angles of those polygons must equal 360°. It follows that only polygons with internal angles of 60°, 90° and 120° can fulfill this requirement – equilateral triangles, squares and hexagons. The pentagonal tessellation above can be seen to contain both four 90° polygons as well as three 120° polygons.

The note above on Cairo tiling illustrates one particular tessellation that has gained some notoriety. It is shown immediately above as the pentagonal tessellation, one of – it is so far believed – fourteen different tessellations it is possible to lay out with an irregular pentagon. You should be aware that the pentagon shown above is not a regular pentagon. A regular pentagon can not be tessellated. This is easy to prove as the internal angle of a regular pentagon is 108° and, if rotated about one of its corners, as is illustrated on the far right, three positions will be described by 324°, which is 36° less than 360°. Hence, there is no contiguity. On the left, a Cairo tile is shown for comparison.

While the comments above relate to the construction of tessellations using a single type of polygon, it is also possible to construct tessellations with a mixture of types of polygon, usually equilateral triangles, squares, hexagons, octagons and dodecagons in different arrangements. The polygons illustrated here in this first diagram have sides of the same length.

The next three diagrams illustrate the only ways in which combinations of two different polygons can be put together without leaving spaces. This first diagram illustrates two combinations of polygons utilising, on the left, equilateral triangles and squares and, on the right, hexagons and equilateral triangles.

This next diagram illustrates the number of ways in which two different polygons, in this case, on the left octagons and squares and, on the right, dodecagons and equilateral triangles may be combined to cover an area without leaving spaces. They show a relatively simple way in which the angles adjacent to the meeting planes are filled to close the patterns.

Finally, the third diagram shows the number of ways in which three different polygons may be combined to cover an area. On the left a dodecagon, hexagon and square are combined while, on the right a hexagon, square and equilateral triangle have been arranged to cover an area.

There are no other combinations of regular polygons which can be combined in this way, although there are a number of other ways in which shapes can be assembled to cover an area. Those with an interest in these patterns would be well advised to look at the work of Maurits Cornelis Escher.

This illustration shows the most common form of tiling which can be developed based on a square grid, shown here defined by the background red lines. The way in which these contiguous tiles are formed is by ensuring that any shape taken out of the basic square, is added on to its opposite side. In the left hand example there is a reflexive curve running along a single edge of the central tile and which is repeated on all its edges. The central example is a more extreme example of the first example and the right example is similar, but uses straight lines instead of curves to create the final tile. You will see that, when examined against the pattern types above, this pattern accords with type P1.

The patterns above were created by establishing, on each line forming a side of the square, an even number of elements, two in these examples, displaced in opposite directions at right angles to the line – essentially a reflex curve in the first two examples, with this being repeated on all four edges of the square.

But if the line is divided into an odd number of elements, three in this case, then a different character of pattern emerges. The reason for this is that it is not possible to nest the tiles immediately horizontally and vertically due to the character of the odd-numbered shapes forming the tile’s edges. Instead, and in this particular case, the adjoining tiles have to be turned through 90° in order to nest. The resulting pattern is illustrated here, the rotated tiles being shown with a slightly different tone of blue. Note that this pattern may be turned through 90° and will still appear to be the same pattern.

In this example of an overall pattern, the horizontal rows of tiles are exactly the same as the above example in that they are composed of tiles alternating with tiles rotated through 90°. However, the pattern illustrated here shows an alternative way of nesting the horizontal rows together, the rows being moved a third of a tile horizontally in order to make a fit. You will notice that the tiles of one orientation now touch each other along two thirds of their length compared with those above which touch only at their corners, forming a strong diagonal line at just less than 72° to the horizontal, compared with the looser pattern of the example above where the diagonal is established at 45° to the horizontal. Note that 72° is a fifth of the internal angle of a pentagon and the internal angle of a segment of a regular pentagon.

more to be written…

go to top of page

Artisans and geometry

Here, below, is evidence of such activity in this page taken from a Persian document, written between the eleventh and thirteenth centuries, whose author is not known, and entitled ‘Fi tadakhul al–ashkal al–mutashabiha aw al–mutawafiqa’– ‘On interlocking similar or congruent figures’.

There are two points I would like to make here relating to the diagram. The first is that it appears to support the argument that geometric studies such as this might have been made, or might have been used, to record or investigate geometric tiling patterns. The rationale for this has been suggested by a study of the translated document which holds that the document, in its lack of structure and differing quality of work, appears to be the work of a scribe noting conversations held between mathematicians and artisans, rather than a geometric treatise or artisans’ handbook.

The second point has perhaps more to do with my possible lack of understanding of the diagram. The diagram on the page appears to show a single quadrant each of a twelve-point – lower left, and a ten-point – upper right, geometrically divided circle, each of which touch at a point. To its right is a simplified illustration of the diagram.

In this first illustration I have crudely assembled a number of the full patterns to give an indication of how the diagram might have been used in a tiled wall or floor design. It shows horizontal runs of ten-point and twelve-point stars though it is possible, of course, that the stars might have been assembled in any number of different ways, creating different effects.

But referring back to the initial page and the simplified diagram I have made to its right, there appears to be an anomaly. This can also be seen in this, second, simplification of the pattern. In it you can see that the points of the twelve-point stars at three and nine o’clock don’t meet as they should, and that the stars are irregularly shaped. There is a reason for this.

Elements A and D belong to the ten-point star, elements B and C to the twelve-point star. Elements C and D have regular points in that the two lines of the star pointing outward have equal lengths. But you will see that the lines forming the points of elements A and B are of unequal length and, although you can’t see it, the construction appears to have been forced in order to have the ten- and twelve-point stars touch. So far I have not been able to work out exactly how the geometrical construction has been derived and will re-write this when and if I do.

To reiterate the main point I wish to make here, it appears that there was significant study made of tile patterns and their underlying geometry, and it seems highly probable that there is more to learn about the methods of tiling as suggested by the work above on girih tiles.

Moving off subject a little, and to illustrate something of this, here is a small detour into one of the issues relating to the way in which these designs can be amended to produce different results. First, here is a repeat of the pattern above, but with two of the five-pointed stars indicated more strongly. The significant element to look at are the arms which create the twelve-point rosette. Note that they are not quite parallel but are narrower towards the outside of the rosette.

Here is a second version of the pattern above, apparently the same, though with a significant difference. Again, two of the five-pointed stars have been coloured to aid a degree of comparison. First, note that the arms which create the rosette are arranged in parallel pairs. Secondly, whereas the twelve-point rosette above is constructed of three, four-point stars, the lower rosette is constructed of four, three-point stars.

These amendments to the design of the twelve-point rosette create five-pointed stars of a very different shape from the original pattern and a slightly different feel in the whole design. Note the two blue lines in the lower detail which show how the stars have lost something more of their regularity, although this could be amended by small adjustments to their arms. These small details are the kind of elements which those constructing the patterns would have at their disposal.

Here, for what it’s worth, is the same pattern, but with all the joining elements added to complete its overall design. At this scale, the eccentricities of the stars are not apparent, though the horizontal character of the rows of decagons and dodecagons is more apparent, a possible difficulty if the designer wishes to have a pattern which appears to be evenly distributed in two directions across the plane.

go to top of page

The appearance of the circle

Very rarely in Islamic geometric design is the circle apparent as such. There appear to be circles in many of the designs, and approximations of the circle can be seen in geometric patterns, but these circles are formed from the straight sides of polygons. As is illustrated here, for a given diameter, the greater the number of sides to the polygon, the more likely a circle is to be approximated. Yet the circle is the generator for most if not all geometric forms. These polygons have sides of, reading from left to right, 3, 4, 5, 6, 7, 8 and, on the lower level, 9, 10, 11, 12, 15 and 20. You can see that the last one is very nearly a circle.

There are some who claim that a circle is not needed in deriving or forming certain patterns, but others argue this not to be so. To some extent this is a semantic argument as a circle, or at least a pair of compasses, is necessary to construct any shape in order to form right angles and to sub-divide angles.

go to top of page

Numbers in Islam

In discussing Arabic geometry concentration so far has been on the basic geometries relating to the construction of two-dimensional shapes – the elements from which patterns are established and assembled in Arabic tilework and similar decorative materials. But there are related areas that receive little attention in the West, those of

• numbers – in their relationship with pattern and geometry, and
• numerology – the divining of meaning from numbers.

There is considerable discussion about the rationale behind numerology, with many claims made for it as a science – and as a pseudo-science by its detractors both in the West and those who have come to it from an Islamic perspective. Just as there are those who argue for the significance of certain numbers in the Bible, particularly seven, twelve and forty, there are Islamic scholars who argue the significance of four, seven and nineteen in the Quran.

In this context I should add here that my understanding of the number ‘forty’ is that it is used to signify a large undefined number, perhaps as we might today say ‘thousands’ or ‘millions’, but not meaning it in an accurate or literal sense. The importance of the number ‘four’ may also be an influence in the use of the number ‘forty’. Bear in mind that, in those days, many people could not count, and shepherds customarily using systems relying on stones to keep a register of the numbers of their flocks. It is also notable that the number ‘forty’ appears many times in the Bible…

go to top of page

Four

The number four is also one which regarded as being important in the Islamic world. As with the numbers seven and nineteen, it’s difficult to know where to start. In no particular order:

• the creation of the earth took four days,
• the name, Muhammad, appears in the Quran four times,
• the name of Muhammad in Arabic has four consonants,
• there are four Archangels, Jibril – who revealed the Quran to Muhammad, Mikail – the Angel of Mercy, Israfil – who will signal the Day of Judgement, and Izra’l – the Angel of Death,
• there are four sacred months in the Islamic calendar. They are the twelfth to the third months of the Islamic year – Dhuw al-Hijjah, Muharram, Safar and Rabi’ al-Awwal. The name, Rabi’ is derived from the word for four. Curiously to a non-Muslim, Rabi’ al-Awwal, or Rabi’ the First is named as such as it is the fourth of the sacred months. The month which follows it is Rabi’ al-Thani, or Rabi’ the Second, so named as it is the fourth month of the calendar,
• the creation of the earth took four days,
• there are four rivers in Paradise; they are of water, milk, wine and honey,
• relecting the four rivers of Paradise, Islamic gardens are traditionally divided into four parts by water channels,
• there are four cardinal directions,
• and four elements of nature,
• and so on…

As I have mentioned before, the point of this is solely to demonstrate some of the sources which give rise to the importance of the number four in Islamic thinking.

go to top of page

Seven

There are many references to the number seven in the Quran. It is a number which has, because of this, not only its usual numeric value but also important symbolic meanings.

According to the Quran, God created seven heavens – 65.012:

Allah it is who hath created seven heavens, and of the earth the like thereof…

To those who observed the heavens there appeared to be seven bodies which were important to them and could be seen with the naked eye:

• Saturn,
• Jupiter,
• Mars,
• the Sun,
• Venus,
• Mercury, and the
• Moon.

These they perceived to sit and move each on their own ceiling above the earth. They might be envisaged as a nested set of geocentric ceilings each supported on invisible columns, with the stars attached to the lowest of these ceilings - 67.005:

And verily We have beautified this lowest heaven with lamps…

According to a hadith there were also seven phases through which the Prophet, guided by Gabriel, made an ascent to Heaven meeting, at each stage respectively, Adam, John the Baptist and Jesus, Joseph, Idrees, Aaron, Moses and, finally, Abraham before moving to the last heaven where there were four rivers, two within – the rivers of Paradise – and two outside – the Nile and Euphrates. It is not my intention to discuss these in any detail. My only purpose is to note that these numbers exist in the Quran and hadith, and must be considered significant.

The number seven is found in many Islamic buildings including, for instance, the Hall of the Ambassadors in the Alhambra, Granada where, with the number four it appears all over the room. This space, like many of those in the Alhambra, was designed for quiet and contemplation. It is a space where the observer may bring himself closer to his God through spiritual reflection. It is significant, then, that the number seven was considered important enough to be integrated so strongly into its decoration.

As obtains with the number nineteen, mentioned below, there are a significant number of coincidences relating to the number seven in the Quran, and which have been the source of interest by Islamic commentators:

• the number of words in the first and last verses of the Quran is 7 each,
• the number of words in the first and last suwar of the Quran is 49, or 7 x 7,
• the number of suwar which have verses being a multiple of 7, is 14, or 7 x 2,
• the number of letters used as initials are 14, or 7 x 2,
• from sura 1 to sura 112, where the name for God appears first and last, there are 112 suwar,
• the number seven is the first number mentioned in the Quran,
• the first chapter of the Quran is composed of 7 verses, and the
• number of times the letters of God’s name occur in this opening sura of the Quran is 49, or 7 x 7,
• and so on…

There is a large body of study into the mathematics of coincidence, or theory of probability, and I do not intend to go into it here. The purpose of setting out some of the above coincidences is solely to establish the interest there is in the number seven.

go to top of page

Eight

The number eight is referred to in the Quran where, in sura 69, al-Haqqah, it is stated to be the number of angels who will support the throne of Allah on Judgement Day. This number is argued to be the rationale behind the design of many elements of traditional architecture and related artefacts that are based on octagonal geometry.

The hadith also give the number of levels of paradise and the gates into heaven as being eight, each having a discrete name identifying the history of those individuals entering heaven.

This number is expressed through the geometry and patterns described by the octagon and eight-pointed star.

go to top of page

Nineteen

With regard to the importance of the number 19, sura 74:30 of the Quran reads, simply:

Over it are nineteen.

Some translations have this as:

Over it are nineteen angels.

though the word ‘angels’ doesn’t appear in the Arabic and appears to have been introduced in order to make better sense of the sura.

There seems to be uncertainty as to what the quotation means as the suwar of the Quran are not set down in the order in which they were received. This gives rise to speculation about how this verse might read in relationship to their original reception. As the ordering of the verses is ascribed to Khalif Uthman and not Muhammad, then arguments relating to the numerology based on the present order of verses are unlikely to be sound.

For instance, it is known that the first revelations received by Muhammad were the first five verses of Sura 96 followed by verses 17 to 30 of Sura 74 which ends with the quotation given above – ‘over it are nineteen’. It is argued that 5 verses plus 14 verses add up to 19 verses; hence the verse ‘over it are nineteen’.

This has led scholars to look for instances and relationships in the Quran having nineteen as a basis. There are a wide variety of combinations of counts in the Quran which, it is claimed, are divisible by nineteen. For instance, the

• Quran is composed of 114 suwar – 19 x 6,
• the Quran is also composed of 6,346 ayyat – 19 x 334,
• the first revelation made to Muhammad comprised 19 words, and
• these 19 words contained 76 letters – 19 x 4,
• the number of suwar in which the word ‘God’ appears in the Quran is 118,123 – 19 x 6,217,
• the phrase that begins every verse of the Quran has nineteen different letters in it, excluding repetitions – in English this is usually translated as:

In the name of Allah, the most gracious, the most merciful

• the word ‘name’ appears in the Quran19 times,
• the word ‘God’ appears in the Quran2,698 times – 19 x 142 times,
• the phrase ‘the most gracious’ appears in the Quran57 times – 19 x 3 times – half the number of suwar in the Quran,
• the phrase ‘the most merciful’ appears in the Quran114 times – 19 x 6 times, the same number of suwar in the Quran,
• 19 associates the first and last cardinal numbers, 1 and 9, and
• 19 is the sum of the cardinals, 9 and 10, as well as the difference between the squares of those two numbers – 100-81.

These relationships or coincidences have led to claims of conclusive proof that the Quran can only be the work of God.

I don’t intend this list to be fanciful but a search on the Internet will turn up even more examples of the perceived importance of the number, nineteen:

• Halley’s comet appears every 76 years – 19 x 4,
• the human body contains 211 bones – 19 x 9,
• a full term foetus develops 266 days or 38 weeks after fertilisation – 19 x 14 and 19 x 2 respectively,
• and so on…

It is not my intention to try to promote or disprove the importance of nineteen, solely to mention that it is deemed important by many Islamic scholars, and reinforces the importance that numbers have in Islam.

Having said that I should also add that it appears that all religions place significance on certain numbers, though the numbers differ with the different religions. One, three, five, six, seven, nine, twelve, seventeen, twenty-six, twenty-eight, thirty-six, forty-nine, one hundred and twenty-eight, one hundred and forty-four, one hundred and fifty-three, six hundred and sixty-six, seven hundred and eighty-six and so on are all numbers believed to have a meaning beyond their functions as elements of counting.

go to top of page

Colour

It might also be useful to mention the theory of Islamic colour dealt with here where it is related to the numbers three, four and seven as well as to other factors. Essentially it holds that the Islamic system of colour arranges colour on three levels:

• a system of three colours, and a system of four colours,
• a system, based on the first, of seven colours, and a
• system of twenty-eight colours based on four times seven.

The system of three colours comprises:

• black,
• white, and
• sandalwood.

The system of four colours comprises:

• red – representing fire,
• yellow – representing air,
• green – representing water, and
• blue – representing earth.

These seven colours are also associated with the seven heavenly bodies. Based on an Egyptian system, it holds that:

• Saturn is associated with black,
• Jupiter, sandalwood,
• Mars, red,
• the Sun, yellow,
• Venus, white,
• Mercury, blue, and the
• Moon, green.

more to be written…