
a collection of notes on areas of personal interest
- Introduction
- Arabic / Islamic design
- Arabic / Islamic geometry 01
- Arabic / Islamic geometry 02
- Arabic / Islamic geometry 03
- Arabic / Islamic geometry 04
- Islamic architecture
- Islamic urban design 01
- Islamic urban design 02
- Islamic urban design 03
- Islamic urban design 04
- Islamic urban design 05
- Arabic / Islamic gardens
- Gulf architecture 01
- Gulf architecture 02
- Gulf architecture 03
- Gulf architecture 04
- Gulf architecture 05
- Gulf architecture 06
- Gulf architecture 07
- Gulf architecture 08
- Infrastructure development
- The building industry
- Environmental control
- Perception
- The household on its lot
- A new approach – conceptual
- A new approach – principles
- A new approach – details
- Al Salata al jadida
- Public housing
- Expatriate housing study
- Apartment housing
- Pressures for change
- The State’s administration
- Society 01
- Society 02
- Society 03
- Society 04
- Society 05
- Society 06
- History of the peninsula
- Geography
- Planning 01
- Planning 02
- Population
- Traditional boats
- Boat types
- Old Qatar 01
- Old Qatar 02
- Security
- Protection
- Design brief
- Design elements
- Building regulations
- Glossary
- Glossary addendum
- References
- References addendum
- Links to other sites
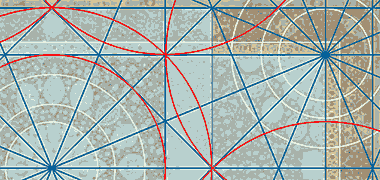
A background to two-dimensional design – geometry and pattern





When we see patterns such as those illustrated on these pages, we recognise in them an association with Islamic geometry, the geometry of the Islamic world. By extension we think of the mathematics required to produce these geometrical patterns. Yet it would be wrong to ascribe our knowledge of mathematics to the Islamic world as it was, to them, essentially a necessary function associated with a need to build, or engineer from which patterning was developed expressing beauty within their religion. Mathematical theory, and the associated structuring of patterns, was introduced by the Greeks, notably by Euclid, around 300 B.C. and further developed in the Islamic world along with other sciences.
However, geometry is one of the main characteristics that distinguish Islamic artistic designs. It creates an immediately recognisable identity, one that is founded in an all-embracing philosophical and cosmological approach to the creation of designed and constructed works, contrasting multiplicity and unity. It honours nature in an abstract decorative art, and brings benefit through its lack of restriction by the constraints of a numerical system.
A brief introduction to the history of Arabic or Islamic geometry has been started on the next page together with methods by which those geometries can be readily constructed using the traditional means of a straight edge and a pair of compasses, though it will be seen there are some limitations to that method, and that it is not clear how some complex patterns might have evolved.

These first six illustrations are of Islamic geometric patterns that have been executed on a variety of materials, respectively silver, stone, leather, glazed mosaic applied to a wall, wood and a single glazed mosaic tile. In the design of their patterns they are commonly considered representative of Islamic design. While not demonstrating the wide variety of geometric treatments to be found in Islamic or Arab geometries, they are here to introduce something of the design character and materials that were used in the decoration of spaces in the Islamic world.
But having said that, it would be useful to begin this page with a note on the understanding we in the West have of Arabic or, perhaps more accurately, Islamic geometrical design as it is a wide field of study and there are many misconceptions about its origins, interpretation and character as well as new capabilities to examine and develop traditional patterns, particularly with the aid of computers.
The patterns with which we are familiar are found within a variety of Islamic cultures, but are often considered to be common to areas of Arab conquest. At its simplest, Arab scholarship enlarged our comprehension of underlying geometries, and Muslim craftsmen, not all of them Arabs, relied on this body of knowledge in producing their characteristic fields of tiling, mosaic, plaster and wooden patterns that were applied to elements of their buildings. Generally they are seen as two-dimensional surface treatments, though there are examples of three-dimensional work in many areas of the Islamic world, particularly with the development of the muqarnas.
To develop the argument, the distinction might suggest that the decorative work is considered Islamic when employed in the service of religious buildings. However, with Islam governing all aspects of Muslim life, the argument would suggest that geometric designs, with their inherent character supporting introversion and reflection, should all be considered Islamic.
The first point to bear in mind is that there are three types of patterning common to the designs found in Islamic cultures:
- Arabesque or cursive,
- calligraphic, and
- geometric or polygonal,
the latter of which contains the largest number of examples we are likely to come across, and is the area most commonly examined from the perspective of their mathematical bases. Let’s look at some patterns.

The first example, above, typifies the kind of design that comes to mind when thinking of Arabic geometric designs. However, the example is not from Arabia but was made in France and is one of a pair of silver door panels, shown above on its side. Incidentally, the other panel of the pair, although having the same basic geometric construction, has different detailing as is illustrated here.

In a very similar manner, this photograph also illustrates the centre of a door panel. Based this time on twelve-point geometry rather than the eight-point shown above, there is an evident family feel to the design of the two panels, one that is familiar to many people as characterising their recognition of Arabic or Islamic design. Again the pattern is formed by the use of geometrically arranged ribs set on the same plane, containing foliate decoration, but here with contrasting materials used to emphasise the distinction between the two characters of Islamic design – lineal geometry and foliate decoration.


While many of the designs illustrated here, including my attempts to deconstruct them, are based on two-dimensional designs, there are many examples of three-dimensional design work in the Islamic world. Here to the side is the top of a fifteenth century wooden Egyptian minbar that has been articulated with pendentives, a form of cantilever that is commonly used in masonry constructions, though here is more decorative than structural due to the inherent character of timber which has both compressive and tensile qualities which stone lacks.
The lower photograph here shows a part of the side of the stairs on the same minbar. It illustrates something of the strong modelling that can be created with, essentially, two-dimensional geometric patterns. Note the strong difference in treatment and effect between the simple cursive running design on the framing and that of the main geometrically laid out panels.

There is more written about the basic geometries behind Islamic patterns on both this page and the next page which illustrate some of the constructions behind basic Islamic designs. But it might be useful to introduce here the idea of different geometries being used adjacent to each other, yet remaining in harmony. These panels are from the minbar illustrated above. The panel on the left has a basis in ten-point geometry, while that on the right is twelve-point. These are designed as separate panels and illustrate a simple solution to patterning. Later on more complicated patterns combining more than one geometry in a single pattern will be illustrated.


These next two examples of artefacts exhibiting Arabic geometry have been included even though they are less complicated in their underlying geometry and far more crudely assembled than that above. I have shown them because they are, perhaps, more the type of example with which we are familiar in our daily lives. This standard and character of design is commonly found all over the Middle East. They represent the character of inlaid work that is displayed in many decorative pieces. Sold to tourists many such items are brought back from the Arab world. The lower example, in particular, is extremely poorly set out. Nevertheless, it has sufficient geometrical integrity for the pattern to be easily seen and readily comprehended. Incidentally, all of these first three examples are based on eight point geometry, a common and relatively easy framework to establish.

Mention was made above of three characters of Islamic design, and it might be useful to illustrate something of them briefly here even though they are not really related to the subject of these notes. While many regard Islamic designs as being based on strict geometrical constructions, there are also Islamic designs that are formed with floral devices and where the governing geometry might not be immediately obvious. This first illustration is of a plate with a beautifully articulated design of a ship, the rim being very crudely broken into four panels creating a degree of stability for the extremely mobile centre design.

Compare the above dish with this which has a decorative pattern on it and an apparently eccentric geometrical layout. The rim of the dish is broken into nine, slightly unequal, elements inside which there are six stylised flowers hanging from the central motif which, itself, has nine points in its centre, but ten outer petals. Although the pattern is nowhere as interesting as that of the plate above, the slight eccentricities of its execution give it a certain vitality.

Here is a dish that is simpler, in that its geometry is based only on a division of eight elements, though it has a more complex decorative treatment. The calligraphic decoration reads, I am told, ‘ahlan bikum’, a repeated phrase that bids welcome to the user of the dish. Whatever the reading is, the design incorporates both a form of kufic calligraphy as well as natural decoration that integrate into a pleasing visual design.

This next illustration, again Turkish in origin but more recent in manufacture, is placed here as a reminder that there are other forms of decoration that were, and are still, produced by Islamic designers, this piece being made of a hardwood inlaid with white shell pieces. As yet I have made no effort to analyse this design as it doesn’t really fall within the ambit of these studies, but casual inspection suggests there is an underlying framework governing its design.

However, here is something rather different. This example has been introduced in order to remind and illustrate that not all Islamic design has a geometrical basis to it. In fact this work appears to be completely free-form in its design and is a modern piece of work. The first photograph shows the junction of the wall and floor within the Grand Mosque at Abu Dhabi. It may seem to an outside observer a little out of place in the context of Gulf architecture, perhaps having more resonance with Mughal design. This detail of the wall and floor junction clearly shows there is no geometrical framework behind the design and that it is freeform. Significantly, and another reason for the illustration being here, the flowers in the wall are raised, a technique that encourages the the sense of touch, introducing another sense to the enjoyment of the space and its containing surfaces.


What is even more surprising is the manner in which the design has been allowed to fill the walls as can be gauged to some extent in the second photograph. This is a large masjid and it is evident that the designer has produced a treatment commensurate with the scale of the building. Generally this is not the way in which masaajid have had their walls decorated, geometric tile work usually being confined to the lower part of the wall forming, in effect, a well-defined dado or plinth around it. Here the decoration treats the wall as a single plane, from floor to ceiling, allowing the naturalistic tendrils to move up and sinuously over it though, internally, reaching only around two-thirds of the height of the wall where it surrounds window openings. This is its closest link with traditional Islamic design where the eye was encouraged to move over patterns, finding and re-finding patterns within its infinite two-dimensional geometric base. Here the eye tends to move over the wall in a similar manner, though ungoverned by a geometric basis. It might be argued that there is another difference from traditional geometric designs. In those the geometric basis had an implied infinite basis extending in two directions. Here there is a tendency to read the patterns vertically, horizontal movement of the eye being naturally constrained by the tendrils or stalks. Externally, raised wall decoration reaches considerably higher while the floor of the central courtyard has been given a similar treatment to that of the internal walls of the musalla, as illustrated in the lower photograph.

This next example, that of an embossed and inlaid brass dish in three finish colours, is a more familiar example of Islamic design work but can be seen to have a passing relationship with the freeform design above. Geometrically it is based on an eight-point geometry for setting out its outer cursive decoration, and a six-point geometry within the central area which incorporates and surrounds a simple calligraphic motif. Both geometries have been established from the same horizontal base. The design has a very strong cursive feel to it and might even be thought to be related to Celtic patterns which would have developed considerably earlier.

Before looking at the next few examples of geometrical designs utilising Kufic calligraphy, it might be useful to place here an example of Kufic calligraphy in order to show something of the basis of the geometric work on which it was based. This is the oldest style of Arabic calligraphy, originating in what is now Iraq, its importance reinforced by its being the style in which the first copies of the Holy Quran were written. This example is of early kufic.


Here is a heavily embossed silver dish in a kufic calligraphic style. The calligraphy has been used to create this particular character of work which has a strong geometrical framework controlling the design. At the centre of the dish, surrounding the calligraphic bismillah, there is an octagon surrounded by interwoven strapwork that is extended in pairs towards the edge of the design where it is either returned or developed into the kufic calligraphy. Between the kufic elements of the design there is cursive work that creates the embellishment typical of this kind of work. While there is a general proscription against natural elements you can see in the lower detail that the craftsman has introduced small fish into the design, further enlivening the dish. The design contrasts with the dish above and is placed here deliberately for contrast, these first examples indicating something of the variety there is within Islamic design. Note that the lines forming the points of the central octagon are not established in a similar way to the octagon containing it and formed by the strapwork.

Contrasting with the dish above in terms of its materials, this dish takes the concept of containing geometry a little further in that the geometry is implied rather than overtly laid out. Photographed in the Victoria and Albert Museum, London, the dish is decorated in a kufic calligraphic style. It is at first glance a powerful graphic design, deriving its strength and mobility from the interplay between its heavy vertical strokes, and the enlivening created by the finials of the letters and the fine cursive elements springing from the verticals.

But, as can be seen in the second illustration, the dish has a strong geometry that has been used to establish the positioning of the vertical strokes. While these strokes are not absolutely coincident, it is obvious that the calligraphy has been set out on the basis of the dish having been divided geometrically into twenty divisions, each of 18°, the eccentricities from the geometry presumably having to do with necessary spacing of the letter forms.

This may not be a complete coincidence as another of my photographs, taken at random, illustrates another dish, again which I have divided into twenty divisions, the lines having a fair degree of coincidence with the calligraphic treatment around the rim of the dish, the calligraphy this time sitting on the rim, compared with the dish above, and the verticals of the letterforms being more accurately set out. I should add that I looked at different subdivisions of the plate, but only the 18° divisions, illustrated here, had a reasonable degree of coincidence.

Examples of this form of Islamic art exist all over the Islamic world, executed in a number of different materials. Above there are illustrations of calligraphy on metalwork, parchment and porcelain. By way of contrast, here are two complex examples of naqsh or carved plasterwork organised around a doorway in Isfahan, Iran, both comprising calligraphic and foliate elements in their integrated designs. These examples are known as foliate kufic.

While this form of Islamic design is not geometric in its strict sense, the finished work appears to have a strong geometric content created, particularly, by the strength of its ascenders set against the foliate work. As naqsh, its execution has much in common with chased metalwork, though the latter also commonly contains repoussé work, where the piece is marked from the back. This second example of naqsh, also photographed in Isfahan, Iran, contains an unusual elaboration of the letter ha which creates a visual association with the foliate work while assuring its difference with an alif and kaf.


These two examples of calligraphy illustrate, in general, two different directions calligraphic work has taken, dependent upon tradition and the materials found and used locally. The first of these was seen in Shiraz, Iran and is of thuluth calligraphy, a later and more freestyle form, here executed on glazed tilework. Again, there appears to be no geometric framework behind the designs. However, the ascenders create the appearance of a grid while the cursive letters act as counterfoils to them, reinforced in detail by small, fairly representative, plants including leaves and flowers, introduced as two colours, yellow and red to contrast with the white calligraphy on the dark blue ground. The second example is from the Alhambra in Granada, Spain and shows something of the setting out framework used to establish the calligraphy as well as its geometric inter-twining and naturalistic flourishes – all in a three-dimensional projection from the blue plane.


Perhaps more than the above, mosaic tilework is considered by many to be the material which typifies the character and appearance of Islamic or Arabic geometry. The scale and the degree of accuracy found in shaping and cutting the tiles differs considerably with region and time. These first two examples show something of this variety. The first photograph was taken in 1975 and is a detail of some tilework on a wall in Shiraz, Iran. It can be seen to be extremely crude in its shaping. The tiles would have been made from glazed and fired material, and then clipped to shapes regulated by eye. Nevertheless, this inaccuracy works to give the finished pattern a degree of liveliness and character which differs from tilework which is more accurate in its tile shapes such as that shown in the second photograph. Photographed, also in 1975, but in Isfahan, Iran, this tilework is far more accurate both in the shaping of its tiles and in its setting out.


The Mediterranean basin has, around it, a profusion of tilework ranging from Moorish work in the west, to Syrian and Turkish work in the east and Egyptian work in the south and along with the north African coast. But this was not the origin of this type of work for it originated, and was introduced, via Persia and Iraq most probably from the Indian sub-continent to their east. As the geometry that underlies these patterns is universal, it is sometimes difficult to determine where an individual design might come from but it must be assumed that there is unlikely to be a single source of either geometry or technique, but that examples might have appeared coevally. This first photograph, for example, is of Moorish work from Andalusia, the detail below it, of a fountain based on twelve and eight point geometries, is Syrian.
The next group of examples are all examples of Moorish tile work, this time of panels in the Alcázar in Seville, Spain, the work probably dating from the fifteenth century. The three panels are used here both to illustrate something of the variations that are found within a single building as well as demonstrating different aspects of design in this art form.


This first photograph shows a very formal six-point geometric basis to the pattern, the design being executed to give the appearance of interleaving lines or straps. This type of illusion has been created by the shaping of the tiles rather than by any three-dimensional modelling, but this character of work needs to have relatively heavy or accented joints between the tiles in order for the illusion to work as effectively as it does in this particular example.
The lower photograph, a detail of the wall tiling above, shows in a little more detail, how this illusion is effected. It should be noted that the tiles creating the strapwork are not simple straps but are formed with angled ends as well as centrally located angles in order to define both the dark blue small hexagons as well as the smaller green octagons.

Compared with the patterning above, which has great clarity in its relatively simple geometric design and execution, here is a much more sophisticated design that has to be looked at carefully in order to see patterns within the design that are not immediately apparent. The whole of the pattern is based on eight-point geometry, the design forming a repeating pattern created with white lines or straps on, apparently, a pale green ground – though this is not the case, as can be seen in the detail below. Within this pattern coloured tiles have been introduced to create a larger, secondary pattern. In patterns such as this the eye tends to switch between the two scales of design, a feature which creates the appearance of mobility within the static design. You can also see that the pattern is not regular across this part of the wall, again adding to the mobility.

This photograph is a detail of the above design and again, even at this scale, there is significant visual movement created by the selection of colours and their combination with the pattern. In addition, as mentioned above, the ground colour is not pale green but a mixture of pale greens and blues of similar tone – and supported by the white tiles – which contrast with the darker sepia and blue tiles. This view has been selected in order to show the regular arrangement of the central area of the above photograph – note how the arrangement introduces points of temporary focus as the eye travels over the design.


Here is another type of design that is more sophisticated than it may appear. On first inspection the design seems to consist of a running design of chevrons picked out in just three colours, green, blue and dark grey. From a distance the chevrons look as if they are made up of similar units but, on closer inspection, it transpires that they are alternating horizontal lines of staggered double and single headed elements, each constructed of a fairly intricate design created by the interleaving strapwork.
In fact the lines are made up of the double headed units arranged symmetrically both horizontally and vertically, the single headed element being the residual pattern between them. The resulting shapes are intricate and, on close inspection, can also be seen to use the effect of interweaving to bring even more interest to the pattern. Note how the interleaving effect is more subtle than that in the example three photographs above.

In contrast, and at first glance this pattern appears to be a simple, though detailed Islamic geometrical design. It is an illustration of the lower half of one of a triptych of panels in a carved plaster work found on a wall in the mausoleum of Moulay Idries at Fez, the work dating to the beginning of the eighteenth century.
However, the geometry is significantly more complex than at first appears. Although I have made an attempt to deconstruct the geometry that forms its basis, I believe that there has been a liberal degree of manual distortion of the geometry in order to be able to produce the apparent continuation of lines that characterise the overall design.
The central roundel is divided into 32 parts, the corners are based on divisions of 24 parts, and two other significant circles of rosettes are based on 14 and 10 part geometries, and of which there are sixteen of both – see the diagram below.
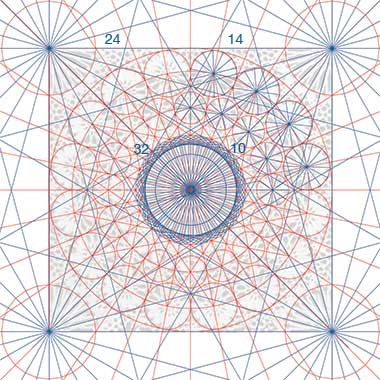
It is difficult to know how the designer went about establishing the basis for the geometry of the panel. Observation of traditional designers in the Middle East has witnessed their using simple line and circle-making equipment, but also supplementing these with formers set at different angles and with markings on them, used to establish important points in the construction of their patterns.
In looking for the method used by a traditional designer, my own preference is to start with the simplest possible connections and see how they relate to the overall design. This illustration shows my first attempt at such a study. Bear in mind that the underlying design is a distortion of the original illustration that aims to make the pattern more or less and accurate square. In particular, note that the ten and fourteen point rosettes do not touch and that, in the finished work, shown first, only a contiguous group of eight and two other points of the fourteen point rosette are completed elements of the pattern.

This detail of the above diagram illustrates something of the problems with the conflicting geometries where it is evident that there is no natural connection between the circles with fourteen and ten divisions, nor with the twenty-four divisions of the corner circles. In order to be able to make the junctions demanded of the design, it appears that the craftsman has had to make a series of decisions involving the moving of the points of junction slightly. While the result might not be thought a ‘pure’ design, it can be argued that it has created a more lively design as the eye moves over the pattern, seeking to resolve the background to its geometry. Having spent some time examining this carving in an attempt to see if the basic decision-making process can be discerned, I am disappointed to have found no sensible result to date.

This is another, similar, pattern in the sense that although it does not have a similar underlying geometry to that above, I have not been able to deconstruct it as accurately as I would like.
Sent to me by a correspondent, the pattern has an attractive and easily read pattern based on eight point geometry with the four octagonal rosettes being linked by decorative bands running through the centre of each octagon. The construction of the octagons is not difficult to understand and set out, but the geometry behind the decorative bands is more difficult to rationalise, although there are a number of ways by which apparently accurate approximations of the pattern might be established.

There are a number of difficulties when looking at the geometry behind the pattern, the first being the exact joining of the four circles in the first illustration of the pattern. The next issue here is a common one – whether the setting out lines run on the side or the centre of the main lines of the pattern. In this case I have assumed they run along the centre, though I am not sure that this is so.
The third issue relates to the extent to which the designer used the natural geometry within the circle to establish the setting out of the visible pattern. While some craftsmen use this method to determine junctions and changes of direction, there is no reason why other methods might not be used. In this case I believe that the latter is a strong possibility, even though I have managed to recreate the pattern, or at least an approximation of it.

As mentioned previously, these first few examples are placed here to give a flavour of the different effects created by designers working with relatively simple geometrical frameworks. There is no attempt to categorise them. While these photographs do not illustrate tiling at the same scales to create accurate comparison, they should demonstrate differing effects for the various distances at which they were taken, this last example showing how animated a static pattern can appear.

While the above pattern appears to be complicated, there are a number of different ways in which the underlying geometry can be set out to create the shape of the basic unit.
This first illustration shows how a basic triangle can be developed to establish the centres of the two arcs required – one inside half the side of a triangle and one outside the other half of the side of a triangle – in order to create a triangular shape that may repeated infinitely, albeit with a second copy that is turned through 60° relative to the first. Having drawn that, there is a second construction which is more likely to have used by a craftsman as it can accomplished with only a pair of compasses and a straight edge.

This second method relies on six-point geometry, where a series of interlocking circles can be set out from a single horizontal line, the compasses being used to draw an initial circle and then drawing equally sized circles centred along its circumference. This rosette of circles can then be developed infinitely, if needed though, in the construction of a tile, it is only likely to be used for a single tile.
The star and hexagon positioned within the spinning trefoil are added by simply joining points of intersection. While this example has only two background colours, it is easy to see how colouring the trefoils in different colours creates a more lively overall pattern as can be seen in the example from the Alhambra immediately above.
From a designer’s point of view, there are a number of ways in which this spinning star pattern might be developed, one of which is illustrated in the next four graphics. While the illustrations above have the pattern using the same trefoil, with an alternative, coloured beige, rotated 30° and nesting with no ground colour between them – the rotation being centred on one of its corners – this pattern is developed by having the trefoil shape mirrored along one of the sides of its containing triangle, creating a space between the two, mirrored trefoils. For simplicity, the construction is not shown, but it is not difficult to establish.

The second of these graphics illustrates one way in which the trefoil shape might be developed into a design pattern. Here groups of six trefoils are arranged within a regular hexagon, open ground spaces being established between the original and reflected shapes. It will be apparent that the arrangement within the hexagon is irregular, mirrored about the central, vertical axis of the hexagon.

It is more apparent in this single-coloured pattern that two different white, spaces have been created by exposing the white ground. Here you can see something of the fluid or natural movement of the design, where the eye is able to move across the field at will. The design can be compared with the example from the Alhambra, immediately above, which relies on hexagons and six-pointed stars for interest and movement, but both being within the basic trefoil giving the pattern a lively feeling withe eye tending to roam freely over the pattern.

The ground spaces in this version of the pattern have been given different colours in order to bring additional interest and movement to the design. However, adding more colours to the two shapes brings a different feeling to the pattern as can be seen in this last of the four graphics. Here the advancing reds first catch the eye as a static arrangement, and then the eye moves to the different colours below the red, tending to view each of the colours as discrete patterns.
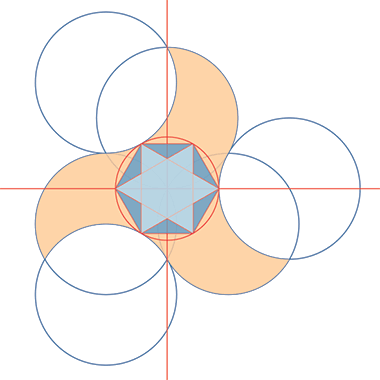
Finally, in looking at aspects of this group of patterns, here is one method by which the geometry behind the hexagon and hexagonal star within the Alhambra tiling, shown a little way above, might be set out.
On the basic layout shown above, draw two intersecting lines, shown as red on this sketch; the horizontal one through the centre of the right hand, blue, circle and the vertical one through the top of the equilateral blue triangle that lies on the points of the spinning trefoil.
From the point of intersection of the two lines draw a circle which touches the circumferences of the three blue circles. From those three points there are a number of ways in which to construct both a hexagon and a six-pointed star, these two shapes being incorporated into the pattern above, found within the Alhambra.

These next two examples are of different types of tilework. The first is an example of what is known as cross and star tiling, a simple form of interlocking, and comes from thirteenth century Kashan in Persia. While the shapes of the tiles have a strict geometry in order to fit together, their internal designs have a more free structure, though still within a framework of four and eight point geometry. Note that one of the patterns has its geometry rotated through 22.5° to the normal.

The last of these three tiled examples is of a single, large carved and glazed earthenware tile from the tomb of Buyanquli Khan, Uzbekistan, and dated 1358. In three colourways – brown, beige and turquoise – it has a heavy three-dimensional modelling created by carving into an earthenware panel up to 20mm in depth. Despite a number of eccentricities in its geometrical layout, it demonstrates considerable mastery in its design, construction and firing.

This photograph illustrates an example of eight-point geometry though it may not appear at first sight, and to Western eyes, particularly Islamic in character when compared with the examples above. It is in fact an original English example of tatting, a practice very similar to crochet work, and was designed in conformance with traditional English styling for this particular character of knotting. What is notable here is that while the two-dimensional design pattern depends to some extent upon Western traditions, there is still a hint of natural Islamic geometry to be seen in the design with the natural, cursive forms following, and contrasting with, a more rigid geometric setting out. But, on more detailed examination, there can be seen to be an active interplay between geometrical layout and constructed detail, a characteristic of much Arabic and Islamic geometrical work, and the reason for its being used here as an illustration.

Finally, here is an example of a metal plate that’s around 250mm in diameter and has been heavily decorated with an intricate and relatively sophisticated Islamic patterning. Its design has elements that can be seen in some of the other decorated material preceding it, and it is placed here as it shows an interesting combination of both geometrical and cursive designs, each of the geometrical elements of the design having decorative patterns set within them.
Looking closely at the design it can be seen that the decoration is extremely detailed and, at first glance, appears to have been produced mechanically rather than by an individual hand. I believe the plate may have been produced for the Museum of Islamic Art in Qatar, but was seen on display at an exhibition in England.

The overall pattern has been laid out based on eight-point geometry, the outer band containing eight circular elements, each alternating with a semi-circular element that appears to have been established on a similar geometrical basis.
The circular elements have two, alternating eight-point designs within them, contrasting with the semi-circular ones which each contains the same figurative design.
The next two bands are divided into twenty-four twelve parts, while the inner band and central feature are divided into twelve parts. Working from a photograph, it has been difficult to make an accurate analysis of the design, particularly the points at which the setting out geometry has been derived. The impression is that different centres have been used to set out the pattern.

This illustration of a detail of the plate shows how the setting out differs with three of the elements of the design. Highlighted are some of the running designs where it is possible to see that in some cases they bands touch one another, while in others they are coincident. The bands comprising the revolving twenty-four squares neither touch nor are coincident with their containing circle, nor are the bands’ centres on the centre of the circular band.
Craftsmen and their work

The design work carried out on the old buildings was usually the work of specialised craftsmen working to the direction of a master builder, a man specialising in the construction and decoration of buildings. It is difficult to know what might have been presented to clients for their approval, but it is likely that the style and extent of decoration was left to the master builder, though perhaps within a financial constraint. The development of the residential compound for Sheikh Abdullah bin Jassim al-Thani at feriq al-Salata in Doha was carried out under the supervision of a master builder brought in from Bahrain, Abdullah bin Ali al-Mail. He would either have brought with him, or selected in Qatar, the team for the construction and detailing of the building. The buildings were, however, relatively simple in design, though there was painted timber and naqsh which would have required specialists.

Elsewhere in the Arab or Islamic world more skill was required in articulating the applied designs, particularly those associated with materials such as tile work, one the main areas associated with Islamic design. In the two photographs associated with this note, young craftsmen work on a design being used to decorate, I believe, the Jordanian Embassy in Qatar in 1988.

Based on eight-point geometry, the design is relatively complex with a high level of detail which has to be accomplished using cut pieces of glazed ceramic tiles. Here, one of the craftsmen is selecting pieces of the tiles for insertion into the pattern which has been marked out on the floor. The tiles are being inserted face down and the back of the panel will be reinforced and then lifted as a single element into position. It may seem strange to see the mechanics of the process with the cut elements sitting in a pieces of brown paper, but this is a highly skilled process requiring considerable understanding of the manner in which each pieces sits in the matrix, and its relationship within the whole design.

Here is an example of a more simple design which was seen being marked out on the floor of a mosque in Shiraz, Iran in 1977. The design has been sketched using pencil and you will note that the setting out is considerably simpler than most of the work I have put on these pages. The reason is simple. Designers know how to make the angles they wish using relatively simple resources. What is particularly noticeable on this floor pattern is that there are no circles nor arcs described. It was all set out with wooden formers set to specific angles.

By contrast here is a craftsman working in the pre-cast factory, north of Doha in 1983, using dividers to set out a panel which will eventually be used in the production of pre-cast naqsh panels for the new Diwan al-Amiri project where traditional naqsh patterns were incorporated into the panels as a characteristic of traditional regional architecture. The naqsh panels owe their decorative treatment particularly to the use of circular patterns set out with compasses, and I have never seen formers used in the production of their designs.
Craftsmen take benefit from those who have gone before them. Formers are handed down or copied, methods observed and utilised as needed. Repetition creates the need for patience and, just as there can be a mesmeric effect in observing Islamic patterns, there may well be something similar experienced in their laying out and construction.
A study of an old panel

Considerable work has gone into the design and construction of this inlaid panel. It was probably made as the top of a chest or box and constructed of wood with an ogee sectioned edge, then covered in small scale inlay work set within a series of defined bands. I am unable to say where it came from, nor suggest its age, though I know it to have been found in the Gulf and is at least fifty years old. It is unlikely to have been constructed there but may have originated in any of a number of different parts of the Islamic world. I have no idea what it covered or was intended to cover.

At an overall size of around 550mm x 380mm the detail which covers it is small in scale though it is not particularly finely executed work, the lack of contrast in its colours – perhaps a consequence of the varnish used – helping to disguise this to some extent. Its interest to me lies is in the simplicity of the geometric basis of its background pattern – a six-point grid. The central feature, of six identical kite shapes, four of them interlocking, is around 215mm x 120mm.

To give an indication of scale, each of the hexagons which make up the background pattern is around 11mm across, and each contains at least twenty-five and a maximum of thirty-one elements which gives an indication of their complexity. Commonly the way in which these are made is by constructing a bundle of rods forming the pattern through its length, and then cutting the bundle to reveal the individual hexagons. Not every hexagon has the same design. In the case of this pattern there is a secondary bundle containing nine elements to fill the space between each hexagon.

Here is the same pattern with the 60° grid laid over it. There are some misalignments as you might expect, due to the differences between the ability to establish the lattice on a computer with precision, and the manual operation of laying out the design. However, I have not shown all the smaller elements of the individual hexagons as they are too small to be set out, and their construction is evident in their relationship within the basic hexagonal geometry. In terms of their manufacture it is astonishing that the craftsmen were able to fabricate the individual triangles and hexagons in rod form accurately enough to obtain the precision they achieved.

The decorative device which forms the focus of the centre of the panel is very poorly established, suggesting that the manufacture was carried out some time ago when accuracy of the underlying geometry was not considered important. The difficulties arise when there is dissonance between the basic line geometry and decisions taken in order to produce thicker lines. Each of the kite shapes is formed by a thick white ribbon with thinner lines, respectively black and ochre on its inner side, and red outside. This photograph illustrates the junction of the kite on the left with that on the left of the four kites forming the central device.

The first point to note is that the curve on the right hand kite is different from that on the left, though it would make sense for them to be the same. The thin red line shows the curve at the centre of the white band on the right, the blue line the centre of the white band on the left. The thickness of the white band is illustrated by the pair of blue arrows. The white arrows illustrate the thickness of the combined white bands at their junction. For the geometry to work correctly, these two thicknesses would have had to be the same. Were the two bands to be coincident at their meeting, then the black line would have lost much of its form, hence the apparent decision to move the bands apart.

This sketch compares the two ways in which the basic pattern can be set out. That on the right shows the relationship which forms the basis of the pattern on the centre of the decorative panel above. Note that the two lowest circles are smaller than the others, requiring different centres, and that they touch each other rather than overlap to occupy a common width as does the pattern on the left.

If, instead of a version of the geometry on the right, above, is selected and the more accurate version on the left is used to create the basic pattern, then the illustration to the right is the effect that would have been produced. Each of the kite shapes is the same and is capable of being nested at right angles to each other without disturbing the underlying geometry. This is not an uncommon pattern in the Islamic world.

This last sketch illustrates how the above pattern would have looked with the additional colours of red, black and ochre lining each of the kites. In fact it is only the inner side of the kites which contains the black and ochre lines, the red line only is carried around the outside of the amalgamated grouping of kites, tying the design together. However, note that the tail of each of the kites is not as well defined as in the original example perhaps, as mentioned above, the reason for the distortion of the geometry.
The construction of a fan pattern


This pattern and its construction have been added as it relates to tiling seen on a new or refurbished building in Doha. It is a traditional pattern, very easily constructed, but not one that was commonly found in the peninsula – though more readily found in regions to the north and east.
The underlying geometry consists of a grid of aligned rows and columns of mutually touching, equally sized circles, with a secondary, similar grid slid horizontally and vertically by the distance of the circle’s radius. The grid this produces allows the creation of the basic fan pattern.
Selectively colouring the fan-shaped elements results in a pattern which has been said to resemble fish scales. This lower image illustrates how small amendments made in selecting and colouring the fans can result in radically different patterns. And by increasing the numbers of colours, or creating more intricate designs for each tile, a wider variety of patterns may readily be developed.
A study of some twelve-point panels
This next group of illustrations are based on a trio of panels displayed together in the Qatar Museum of Islamic Art. Each of them is a beautiful example of Islamic or Arabic geometric artistry, and I believe they are well worth study to determine the geometry on which they were based. Further down the page there are illustrations of how simple geometries are constructed – for those who are not familiar with geometrical systems – but here I have shown them in their complexity as patterns I find attractive.


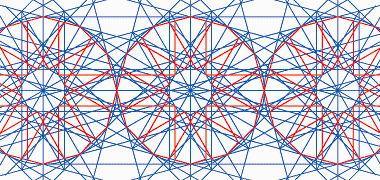

Here is the first panel showing its design and framing, the end frames featuring a small running design. The most probable reason for this extension to the length of the panel is the need to make up the difference between the proportion dictated by the geometry and the requirements of the opening into which the panel would be used.
The first panel is based on a run of circles containing figures set out on the basis of twelve-point geometry, the circles mutually touching on their circumferences and located along a common straight line. In fact there is a central circle flanked by two semi-circles providing the basis for the pattern but, in common with many such patterns, the geometry has to be extended beyond the panel in order to establish all the necessary lines.
In order to construct the basic geometry of the panel, diagonals are drawn at 30° intervals through the centre of each circle, cutting the circumference and being extended. A line is drawn between the intersections of each diagonal with the circumference and extended in both directions.
From the points of intersection of each of these extended lines outside the circle, new lines are drawn across the circle to meet each fifth point of intersection. This produces pairs of parallel lines each side of the circles’s centre. Where these lines cross the lines drawn around the circumference, they will produce the setting out for the red lines which comprise three regular pointed crosses for each circle, producing the familiar twelve-pointed dodecagon.
The three circles producing the basis for this panel can be seen to be part of a pattern of lines of circles regularly aligned at right angles to each other in two directions, as can be seen in the lowest of the three illustrations above.




This second panel has, like that above it, decorative panels at each end, producing a balanced frame to the internal, main pattern. The decorative panels are not running designs as are those on the first panel, but are carefully structured to reflect the proportions of the main design of the panel.
This design bears a resemblance to the first panel in that the two central figures are again based on twelve-point geometry. But this design is created by two small differences in the layout geometry: firstly the circles do not touch and, secondly, their mutual arrangement is designed to be at 45° to the basis of the pattern of the first panel. It is in such relatively small alterations to basic geometry that the apparently infinite variations of Islamic designs are created.
The basic geometry relating to the divisioning of the circle is the same as for the first panel, as well as for the setting out of the lines extending from the intersection of the circumference of the circle with the diagonals. But there is a major change establishing the distance between the circles. This is effected by the lines coinciding with the similar lines of the adjacent circle. The whole arrangement is then turned through 45° to produce the framework for the design of the panel.
This third sketch, based on the layout of the panel, illustrates how the overall pattern produces a very different design from the similar study of the first panel shown above, here each group of four circles having a fifth circle between, but not touching them.



The third of these three panels is very different from the two above. Whereas the central circle is based on twelve-point geometry, its two flanking circles are based on ten-point geometry, and it appears that it is from those that the basic setting out relationships are derived. The distortion of the photograph has been corrected but this has made it difficult to fit the geometry to the image. However, it does allow you to see some of the eccentricities, such as the irregular five-pointed stars between the central and flanking circles created by the slight differences inherent in the two geometries.
Mixing geometries of different bases is not uncommon in Islamic design. The process adds to the possibilities for invention and so enlivens the designs in which it is deployed. In so doing, the underlying construction can become more complex, particularly in establishing the linking shapes. Because of this I have not displayed the continuation of pattern over a wider field, but hope to do so later.
A study of two ten-point panels
The panels above are all based on twelve-point geometry. The two that follow are both based on ten-point geometry and were photographed in Isfahan, Iran, in 1975. Both of the panels were vertical in their original locations but have been shown here horizontally for ease of demonstration.


The first of these two panels was a decorative application to a simple cupboard door set into a wall reveal; the second of the panels was part of a decorative wall installation and is probably the older of the two panels. It is usually difficult to put a date to patterns of this type because of the long history of similar decoration utilising the same materials that will have been in common usage in and around the region for centuries. The cupboard door panel appeared to be relatively recent as it looks as if it used newer materials and the decoration had been added to enhance a more recent functional requirement; certainly it appeared to be newer than the wall panelling which also had a traditional cursive running pattern surrounding the central panel – not shown here – which, together with the greater intricacy of this design, suggested both an earlier design and its fabrication. The degree to which the date of design and construction is likely to be apparent is, to me, impossible to tell, though it is likely to be better understood in the region. It might be thought that there is a correlation between the amount of time and effort expended on a design and its date, but this is unlikely for a number of reasons.
The upper panel was photographed more or less accurately in situ, but the lower photograph has been distorted in order to obtain as accurate a representation as possible in order that a reasonable study can be made of its geometry. For this reason there may be small eccentricities in the study.

While the first panel may have the simpler function and be a more recent panel, it has an interesting geometrical construction. At first glance its basic design appears to be based on two interlocking, lozenge shaped decagons, but this is not the case. The design is focussed on the central decagon, but the wider design is one of a series of decagons arranged horizontally, with a repeat offset to rows above and below. This crude illustration, composed of a series of the above door panel photographs overlaid on each other, shows something of this wider pattern. This is how many panels are constructed – by selecting part of an infinite pattern.



It is relatively easy to show the relationship between the decagons in their individual rows, but not so easy to show the relationships between the rows. In order to construct the pattern, start by drawing a horizontal line and, through its centre draw a vertical line. From their point of intersection draw a circle and, within this circle, construct a decagon – shown here in white – two of its corners aligning with the vertical. Through four of the corners of the central decagon draw lines – shown here in darker blue – to intersect the horizontal line. They will meet at the centre of a secondary decagon – shown here in pale blue which will have one of its sides coincident with the side of the first decagon. Repeat the process to locate the next, white decagon. The centre of one of the decagons on the second, staggered, row will be found at the junction of a vertical line raised through the centre of the secondary decagon and one of the dark blue lines projected through the first, white decagon. The setting out of the lines of the rest of the pattern are readily accomplished by joining points of intersection. What is fascinating about this kind of work is considering whether or not the craftsman who made this would have set out construction lines in the area outside the panel. I have seen large scale patterns drawn on the ground, which might be the way in which this was done – but, perhaps more likely, a copy would have been made from an existing piece of work.

This second panel is set up in a different way, the central decagon being the generator of the pattern around it in a relatively complex manner. It appears that the positioning of the outer group of decagons – the four partial decagons in the corners of the panel – have been determined by using similarly sized decagons – three on each side – overlapping the central decagon, their outer leafs contingent with the inner lines of the central decagon. The partial decagons in the corners of the panel just touch two of this inner ring of decagons, while four more decagons – two horizontally and two vertically, overlap the inner ring of decagons. This is not the usual way I would anticipate a panel being designed, but it gives an indication of another way in which elements of pattern, in this case the decagons, can be established.
The setting out of a five-point pattern

Many of the examples of Islamic design we see around us were designed and constructed centuries ago. But it would be a mistake to imagine that they embody simple geometries in their designs solely due to their having been constructed in earlier times. In fact the geometry of these early patterns can be far more complex than may be apparent on first viewing, a fact which suggests that there was more consideration of the basis of the design than we might anticipate. This reinforces the proposal that there are benefits to be gained through any time spent reflecting on the underlying geometry of much of this work, an aspect of Islamic design on which a little has been written elsewhere.
One such design, shown above and discovered on a web page looking at messages embodied within Islamic geometric designs, is a very good example of the type of complexity underlying what appears to be a relatively simple design. Displayed as two elements of six panels within a framed design, the supporting panels have calligraphic designs which are embellished with arabesque or foliate work, the surrounding frame apparently also being a repetitive arabesque running pattern.

In the case of this fourteenth century Turkish door there are several levels of complexity to consider. Perhaps the most important of these is the hidden message contained within the central pattern and available to those who have the knowledge to read and understand it – an interesting area of study, but one that is not dealt with on these pages.
The overall layout of the door shows an interesting approach to the design of panelled doors. With the knowledge that the central geometry contains a hidden message you might expect the two panels to have been organised to form a stronger element of the overall design. Yet while it is definitely the focus of the door, the central pattern has been deliberately split a considerable distance by both the decorative running design framing the two panels as well as by the decorated ’enf, which appears to be partially missing. Perhaps because of this the design within each of the panels has a slightly fragmentary or partial appearance, suggesting immediately that there is more to read in an expanded view of the geometry and, although I am not qualified to state this for a fact, perhaps hinting at the existence of a message hidden within the design.
The illustration above shows how the pattern on the door accords with the construction outlined above it. There are some minor variations, perhaps caused either in the construction of the door or in the use of the photograph, but the selected elements of the underlying geometric structure can be clearly seen.
These two sketches illustrate the basic underlying geometry which, as can be seen in the left hand sketch, is based on five-point geometry. More can be seen at the link. In particular, the right hand sketch shows this underlying geometry as having been established on five circles, mutually touching and grouped around a fifth, smaller circle. This arrangement is not as easily constructed as may be thought.
In order to draw the basic geometrical arrangement, start with a horizontal line on which is raised a vertical through its centre. The central pentagon can be drawn as set out here, though in this sketch note that it is drawn upside down compared with the sketch above on the left in order to facilitate this particular construction.

Next, extend the sides of the central pentagon until they meet. The five larger pentagons, their size yet to be established, will now each have their two inner sides coincident with these extended lines.
If you have not already created them in the construction of the central pentagon, draw two circles each with their centre at the two upper corners of the central pentagon and with their radii set at the length of the pentagon’s side. These circles are shown in blue.
With its centre at their upper point of intersection, draw another circle of the same radius. The lower point of this circle’s intersection with the vertical line will create the centre for a circle of larger radius to be drawn. This, also, is shown blue.
Now draw two more circles, also shown blue, with their centres on the lower left and right corners of the pentagon and with the same radius – the length of the side of the pentagon. These will intersect with the extended sides of the pentagon.
The large red circle can now be drawn with its centre at the point noted above and with its radius at the points of intersection of the last two circles with the extended sides of the small central pentagon.
Finally, extend verticals from the centres of the lowest two sides of the pentagon through the upper two corners. The points of intersection between these lines and the large circle will be the centres of two of the five surrounding large pentagons. The other three pentagons can be constructed by similar methods used to establish the first two. Note that, in the construction shown above the central pentagon has been reversed about its horizontal axis. In the final illustration, the pentagon sits on its base, rather than on a corner.
This last sketch has been left deliberately vague. While the basic organisation of the pentagons has been relatively easy, the detailed laying out of the constructional lines has not been as easy a pattern to establish in a similar manner to which other patterns have been investigated on these pages. Adding all the lines necessary to enable an accurate selection has proved complicated and is something which will have to be revisited at a later date. It is interesting to reflect on the complication which lies behind what appears to be such a simple pattern.
Pattern selection

One of the many decisions to be made by the designer relates to the manner in which points are joined in the underlying geometery to create the designed panel. This illustration is a simple example of how these decisions can be used to produce different effects, in this case, creating a progression of simple decagonal rosettes that might occur within a more complex design.

The sketch above shows three decagons, the blades or petals of which are of different widths creating decagons with differing areas. It would, in fact, be relatively easy to create more decagons from the same underlying geometry but, for the purpose of this exercise, the illustrations have been kept relatively simple. The underlying geometry is shown here, to the side and can be seen to have a single geometric generation with the outside edges of the petals of the decagon all falling along the same lines. The fine red and blue lines have been added, joining adjacent and opposite corners of the decagon, an exercise which could have been extended to the mid-points of the sides of the decagon, but has not, again for simplicity – though it will be understood that, had this been carried out there would be additional lines within the decagon available for selection. The heavier blue and red lines show the three selections made to produce the first illustrative row of decagons.

This sketch shows a part of the decagon with the fine red and blue lines which join the corners of the decagon evident. The shaded blue areas indicate two of the petals of the decagon. A red circle has been drawn at three different points of intersection in order to show how the designer has available, in this case, three choices which will influence the width of the blades of the decagon. Of course, the blades might be as wide as might be wished for, but by selecting points of intersection, the designer can maintain a geometric logic to the selection and, therefore, to the overall pattern.

Having written above that this note would only look at the definition of three basic decagons, here are three more based on the same sized decagon, but again with the widths of the blades becoming increasingly narrow, and following on from those above. As with the former, these three decagons have been created following lines which join junctions within that same decagon. Not only that, but it is possible to create at least three more decagons with widths increasingly narrow, which would end, logically, with a ten-pointed star.
Lines and width
One of the points to bear in mind when looking at designs is the relationship between the setting out lines and the pattern lines. Many designs are constructed along the setting out lines, but pattern lines generally have width to them and, depending upon the designers’ decisions, there will often be the need to have the pattern lines centred on, or adjacent to, the setting out lines creating both problems and opportunities for designers. The design process has been likened to the setting out lines being the dry bones upon which the flesh is artistically draped, with the designers making a series of decisions in creating their individual patterns.

These decisions are also what are looked for in the investigation of patterns as they need to be understood in order to establish how the geometry was set out. The earthenware tile above is a case in point. It is obviously based on five-point geometry though, as you can see at a casual glance from the two sketches on the right, there may be a hint of a six-point pattern in it. To make matters worse for investigation, there is a significant amount of layout inaccuracy as well but, despite this, the pattern is strong and the layout looks accurate. It is a good example of its sort, a tribute to the strength of Islamic geometrical patterns.



The pattern consists of beaded lines which divide the plane into a series of simple shapes based on five-point geometry. These first two sketches show, firstly, the pattern created by the lines and, secondly, the small infill shapes used to bring character to the pattern. Both these sketches are approximations of the line and shapes and are used only to illustrate the basic pattern; examined in detail, there are a small number of inaccuracies in the execution of the tile which make it difficult to overlay the analysis lines and shapes precisely.
This third sketch, a detail of the panel above, has been drawn to illustrate how the geometry is not constructed as simply as you might anticipate. Given that there is a little distortion in the photograph which accounts for some inaccuracies in the setting out lines, you should be able to see the setting out lines drawn along the main elements of the pattern are not generated from common centres as are most of the others on this page. I have deliberately omitted many of the setting out lines in order to keep the diagram relatively legible, but there should be enough to illustrate the point.

The shapes used in the pattern can be seen in the fourth illustration to the right, and consist of a half pentagon, pentagon, rhombus, triangle and kite plus, not shown here, the make-up pieces at the periphery used to complete the rectangular frame. The basic shapes are used as shown here, but there are some that are mirrored and rotated in order to fit to the pattern. Note that the governing angles in the pattern are 0°, 36°, 72° and 90° from the horizontal, the angles associated with five-point geometry.
Developing a sketch for a cursive pattern
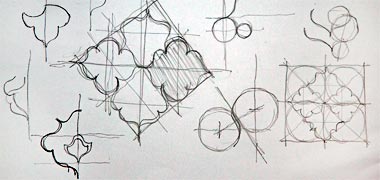

Most of the sketches on these pages have been used to illustrate the construction of geometrical patterns. As touched on above, one of the characteristic types of Islamic art is that of cursive designs which use free form shapes to establish flowing patterns that stand in contrast to the more angular forms established by two and three dimensional geometry. The floral pattern illustrated above is a modern and extreme form of this, but appears to be truly freeform, with no underlying geometry guiding the placing of the elements.
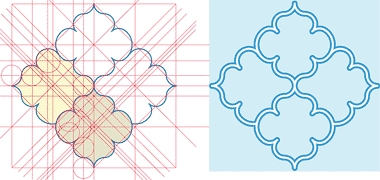
The rough freehand pencil sketch which begins this note was made to look at how the pattern might be established, and was conceived as being best suited to a square tile form with no attempt at a repeat or a junction with adjacent tiles. The design was then developed in a software drawing package, there being no need to return to freehand sketching.
Although freely flowing forms may appear to have little basis in geometry, a significant number of them do so in order to maintain a visual integrity. The pattern to the right, above, is an exercise to illustrate such a pattern which incorporates both an obvious geometric layout with spirals that have elements on them suggesting the stems and attached leaves of plants, features which act in contrast to the more regular geometric shapes and help to associate geometry with the natural world.


The sketches above, and this animated graphic illustrate the relatively simple geometry used to establish the design. This is a design process that embodies many arbitrary decisions in the development of the final pattern. A square is divided into sixteen parts by joining the points established on its perimeter when its sides are each divided into four. That geometry has been omitted here.
Within this square a smaller square is now inscribed, set at 45°, its corners being established on the centre points of the edges of the original square. The smaller square is similarly divided, also into sixteen parts. The lines sub-dividing the smaller square establish the four diamonds upon which four cursive shapes may be designed. These can be seen in blue on the right of the sketch above and are of two similar, but slightly different shapes which fit against each other in what might be considered to be a pleasing and complementary manner.
Inside these four cursive diamond shapes another, simpler, figure has been constructed based on reflex or ogee curves simply constructed around the forms of a number of similarly sized circles which have been established arbitrarily on the underlying grid. This shape is repeated, mirrored vertically and, inverted, horizontally with its pointed and rounded top and base set to contrast with the rounded and curved shapes of the cursive diamonds upon which they sit.


Finally, four spirals have been added, their geometry and placing established by eye while still having geometric connection to points on the underlying grid. On the spirals a few small elements are placed with the connotations of leaves to complete the pattern.
This is by no means a fully worked example, but illustrates a way of designing a cursive design, but one based on an underlying geometry. The associated illustration gives a rather crude indication of how the design pattern might appear when used to cover an area of floor or wall.
The lower illustration is intended to be a more delicate interpretation of the pattern with a pair of tiles joined and the line thicknesses altered along with slight colour variations. Its use would be more suited to graphic work where the refined lines defining the shapes might be better appreciated.
And now for something completely different…

By way of contrast this brief note illustrates a different type of pattern. It is here because, at first glance it may look like a maze or be considered to be Islamic, perhaps because of the obvious visual association with Kufic patterns. But it is not, its geometry has been derived from a squared grid and an underlying eccentricity of decision-making. Its influence was a piece of material noticed in a shop window. Those with an interest in patterns might like to determine what class of pattern it might be.
The design is established on a simple squared grid with the pattern creating a number of broken squares which, like Islamic patterns, move in and out of recognition as the eye roams over it. Rather than explain with a lot of diagrams, this simplistic animation should illustrate how the pattern evolved.

The basic square – light blue – grid has smaller squares inserted into the centres of every other square with each row staggered. The basic square then has two angled shapes added bottom left and top right. Another smaller square is added to the alternate basic squares in their top right corner and angled shapes added with the same relationship to these squares as had the first angled shapes in the basic squares. To finish the arrangement small squares are added between the ends of angled shapes and then a pair of z-shaped forms complete the arrangement. The final brown and red squares are here only to illustrate two of the white squares that can be glimpsed within the overall pattern.
Carpets and rugs

In addition to discovering Islamic geometries on metalwork, tilework, plasterwork and woodwork, we also associate them with carpets and rugs, particularly with Persian carpets that have a long tradition of use in the area of the Gulf and beyond. One of a pair of carpets, the carpet illustrated here in its setting within the Victoria and Albert Museum is one of the most famous Persian carpets, the Aradbil, named after the area in modern Iran from which it originates.
![The Aradabil carpet – with permission ©V&A Images/Victoria and Albert Museum, London [Museum No: 272-1893] The Aradabil carpet – ©V&A Images/Victoria and Albert Museum, London [Museum No: 272-1893]](./islamimages/ardabil.png)
The Ardabil carpet is large, being approximately 1040 x 530 cms, and woven at a density of 49 knots per sq.cm. around 1540 AD. Its central feature is based on eight or sixteen point geometry set in a cursive and floral field with decorative features based on the same geometries in the corner or the surrounding frame. There is an inscription at the top of the carpet, shown on the right in the second of these three photographs.

Looking at the Ardabil carpet, even in these extremely small photographs, you can see how well proportioned it is. Here I have illustrated the geometry upon which the design of the carpet has been based. I will show a fuller geometry, but the key point to note in this sketch is the use of a square in the centre flanked by two rectangles, each having the proportion 1:√2. You can also see how the outer border of the pattern has been established but, again, this should be more clear in the illustration below.

In this study you can see a fuller geometric basis, one that shows the wider setting outside the carpet. This illustrates a point made elsewhere: that one of the chief characteristics of Islamic designs is their continuity outside their encompassing frame. While there are no lineal devices within the carpet to suggest this, there is an implicit continuity outside the carpet that can be sought, and responds to contemplation and reflection.
I have not drawn the stages of construction as they are easily worked out by examining this sketch. Essentially they derive from the central small square upon which a circle is drawn of radius equal to half the diagonal of the square. Circles of the same radius are drawn on the extended lines forming the central square. Connections between the eight encircling circles automatically produce the 1:√2 rectangles that flank the central square. It is also evident from the sketch how the outer edge of the frame is defined, the frame being the difference of the inscribed and exscribed circles relating to the small square.
While the upper sketch illustrates the manner in which the basic shape and the setting out of the main elements of the carpet were effected, I have not yet been able to work out the basis of the setting out of the smaller elements of the pattern, nor of the width of the bands defining the borders, but believe there must have been a rationale to establishing all of them, and that this might be significant. What I have noticed is that the inner motif of the central circular feature has a radius equal to the width of the blue lines defining the border of the carpet. The four quadrant patterns found in the corners of the carpet have the same outer radius as that of the central circular feature, though the inner motif has a larger radius.

In this sketch, I have expanded the geometry of the field in order to create something of the feeling for an infinite pattern within which the carpet pattern sits. In this latter pattern, the frame is derived from the geometry of the overall continuing geometrical field, and might be considered to be placed anywhere within this continuum creating, in effect, a sample from this continuum.

Patterned carpets continue to be designed and fabricated by hand, the finest of them being expensive due to a combination of the materials and the time needed to knot and finish the design. This photograph, taken through a shop’s window, shows a particularly fine knotted silk rug, the main pattern being based on sixty-four radiating lines, though the central lighter ring of shapes are thirty-two in number, and the central star has eight points. It is only with a large number of knots to the inch that a fine design like this can be created.
The key feature of carpets is that they are knotted, a time-consuming and skilled exercise, quality depending upon the number of knots to the square inch. While Persian carpets are objects of desire as well as functional and transportable items of a household, traditionally it was the woven kilim that was the less expensive and more versatile rug to be found in the Gulf. Usually brought over from Iran the most commonly found in Qatar seems to have been those woven by the Qashqai from the region around Shiraz in present day Iran.


Due to the relatively coarse manner in which they were woven, these rugs tended to have simple geometries, a hint of which can be seen in these photographs relating to traditional weaving in the peninsula though, as you can see, they are carried out on a narrow, portable loom producing strips that are later sewn together to produce runners. However it does illustrate the mechanical geometrical form the weaving creates, and also something of the limitations this type of weaving presents. In these two photographs of the corner of a small kilim and a larger kilim, you can see clearly how the woven form creates patterns based solely on right angled geometry, with implied diagonal lines being created by stepping the weave along the warp. The warp threads are those running the length of the carpet, over and under which the weft threads are woven.

Here, the photograph is of the edge of a Qashqaikilim, seen on its side. Although the colouring is not that typical of this type of kilim, the simple running edge detail can clearly be seen to have its patterning derived from 45° geometry, itself derived from the manner of weaving the piece. The patterning in the centre of the kilim also makes use of 45° geometry.

While this type of weaving produced a characteristic pattern responding to the governing geometry of woven rugs, a secondary development saw the use of stepping as a way of varying the 45° geometry. This third photograph illustrates clearly how the angled geometries steeper than 45° are woven. It also shows the characteristic slots created by the return of the weft threads.

In this detail of the centre of a Qashqairug, the characteristic hexagonal form has been used as a feature. This hexagon is obviously not a true geometry with internal angles of 120°, but is an approximation created by the weaver. Nevertheless, the organisation of the pattern within the hexagon continues the feeling of six-point geometry with its incorporation of triangular motifs.
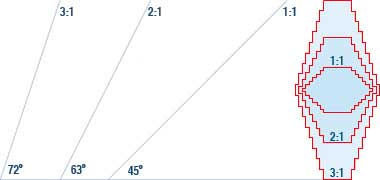
Stepping the weaving is the only method available to create the lines of geometry on a kilim other than those on the horizontal and vertical. Because of this the angles are either right angles or are formed by using different ratios of horizontal weft to vertical warp threads. Note that taking the weft around the warp leads to a series of slits being formed in the kilim – one of its features. This diagram illustrates the angles formed by using ratios of 1:1, 2:1 or 3:1 in the stepping of the pattern. Note that the angle of 72° is related to five-point geometry, and that 63° is an approximation related to six-point geometry.

The stepped element of pattern is a standard feature of woven rugs and can be found all over the world in artefacts, including carpets, using a woven method of manufacture. In Iran and areas adjacent to it in the north and east, there was also a hexagonal pattern developed, similar in some respects to the gulpattern of Turkmenistan tufted carpets, though the latter is commonly octagonal. The kilim shown here is particularly eccentric in its weaving but is here because it displays variations created, most probably, by a novice. The kilim has none of the strong colouring that characterises a Qashqai.

Finally, with regard to rugs, I am including a detail of an embroidered Iraqi kilim to illustrate two points. Firstly, not all carpets and rugs are geometrically based; this kilim is completely covered with non-geometrical images. The second point is, of course, that there are still figurative works to be found in the Islamic world. At the top of the photograph a line of simplified figures can be seen and, below them and on its side, is what appears to be a dancing figure. Elsewhere on the same kilim are stylised birds and camels.
Representative design
Although many people in the West are aware of the fact, it is worth repeating that there is a prohibition against figurative art in Islam through an injunction in the hadith, though not in the holy Quran. The aim is to avoid idolatry. For this reason you will not see anthropomorphic art in mosques and it has been extremely unusual to see figurative art in public places though it is not uncommon in private and there is a long history of it in different parts of the Islamic world, both in secular and court settings. This tends to have been more common in Persia and India where the lack of perspective and shadows has kept the illustrations relatively free from direct representation.

But, nowadays, there is a market for artists producing paintings of the past incorporating their client’s ancestors as well as illustrating stories. It is not common, but there are an increasing number of examples of figurative art being produced for public consumption. I assume this reflects demand and, particularly, the increasing influence of the Western world on general values. This example is of a good quality Persian carpet with the subject matter taken from the stories of Omar Khayyam. Carpets like this are woven for private consumption and can be seen in houses along with similar themes, often paired with pictures of landscapes featuring water, trees and mountains.
This might be thought to cater for the upper end of the market, but there have always been works produced for less expensive enjoyment as in this example above.
Increasingly, however, there is a tendency to represent the past through art in public places – particularly where the past has been irretrievably lost – and this is seen in art work associated with new offices and hotels as well as, and particularly on, roundabouts and in public spaces. Although differing in concept, it is also notable that there are a significant number of portraits of the Ruler and other members of the State or Government in government buildings. There appear to be two reasons for it: firstly the marking of modern achievements of the State and, particularly the head of State and, secondly, the introduction of Western forms in a demonstration of modernism. This art may be seen as a very important reminder of a shared history and a poignant reminder of a need to be seen to ‘progress’. However, it is with non-representational forms that Islamic art is most associated.
Other material

Islamic geometry is featured on a number of materials, perhaps the above examples of rugs and carpets being the most commonly found. Other materials have also been used, such as timber, tile, brick and stone, but soft materials have also been decoratively used to enliven the interiors of buildings. This is not an old piece, being around thirty-five years old, but it illustrates how the application of a simple pattern has been able to bring life to the material both in its geometry as well as its used of heavy embroidery to create that pattern.

The pattern is a simple one, based on a series of similarly sized overlapping circles. The threads creating the design have been hand-worked, given an additional liveliness to the piece. This illustration shows the relationship of the grid of circles to the decorated panel. The main lines of the pattern have been followed but the decorative treatment has been confined to creating lines in blue and gold that follow within the shapes formed by the intersections of the lines.
Sacred geometry and geomancy
Before I continue the notes on Arabic geometry I think it would be useful to mention two other, related disciplines: sacred geometry and geomancy – both of which are related to geometry and both of which have strong associations in the Arabic and Islamic worlds.
Sacred geometry
Since ancient times there has been a deep interest in forms that are considered to incorporate within their intrinsic relationships – both mathematical and geometric – a universal truth. Resonances were considered to be present from the smallest to the largest elements of the natural world and, in this, a unity was perceived. It was believed that these geometries were derived from, or described, the basic laws of the universe and that there was an over-arching hand directing them.
It followed that, by studying or contemplating them, an understanding might be obtained of the origins of everything and, in this, a sacred truth approached or discovered. Conversely, it was believed that these geometries were based on creation itself and that patterns in every field – such as music, mathematics, astronomy or cosmology and natural forms – were derived from them.
As an extension of this discipline it was believed that the geometries uncovered were sacred and, by incorporating them in, for instance, music, art and architecture, these works would have a harmony of proportions and a special sacred character.

One of the early proponents of this thinking was the Greek, Pythagoras of Samos, living around two-and-a-half thousand years ago. Spending time in Egypt and, perhaps, Babylon, it is likely that he learned much from his contact with mathematicians in those two civilisations. Best known for the theorem relating the square of the hypotenuse of a triangle to the sum of the squares on the other two sides, it is unlikely that he was originator of the relationship, though he may have discovered the well-known proof. So-called Pythagorean triples – right angled triangles formed of sides with whole numbers – were known in Babylon a thousand years prior to his dates.
Following his work on numbers Pythagoras went on to investigate harmonies and intervals within music, discovering numerical relations which accorded with discernible patterns. Further work on astronomical bodies persuaded him to propose that there was an underlying numerical pattern to the cosmos, in a sense, a sacred geometry.
While this note appears to accord with general scholarship, the life and work of Pythagoras is clouded in uncertainty. It is known that he named and considered himself to be a philosopher, and that he established a following based on religious practices and rites he developed. What is important is that the work established by him and his followers influenced Plato, born around seventy years after Pythagoras’ death and, through him, Western philosophy.
Following from the above, a secondary definition of sacred geometry would be that which has been used to set out religious spaces and structures, both internal and external. In the Western world the systematic use of mathematical relationships has been developed in both religious and secular buildings, notably by architects such as Palladio in the sixteenth century and Le Corbusier in the twentieth century, the latter developing his own system of mathematical interrelationships upon which to base the preferred measurements for the elements of his architecture.

So, by the beginning of the first millennium there were, in different cultures, substantial bodies of thought supporting the belief that there might be, or was, a central truth governing the natural world and which, when harnessed formally or informally, would benefit all who understood it and, perhaps, even those who didn’t.
When Islam arrived in the seventh century it contained within its central tenets a continuation of pre-Islamic beliefs while encouraging the search for, and reflection on, the concept of perfection. Included within this idea is that there is a sacred geometry, generally interpreted in mathematical terms as culminating in the circle and supporting its geometrical developments.
This connection with mathematics was developed in the next two hundred years, particularly with the Persian, Muhammad ibn Musa al-Khwarizmi, in the ninth century, integrating Greek and Islamic mathematical concepts into a more Islamic framework. Islamic art might be considered to incorporate symbolism which can be seen and experienced in many buildings constructed in areas of Islamic influence. It is argued that this contact with a spiritual art is more important in receiving a sub-conscious connection with Islam than might be obtained through more formal education and instruction; further, that it supports the spiritual character of Islam.
Many of the geometries I describe here relate to this concept of sacred geometry, particularly those relating to the Golden Section and Fibonacci. Looking at the designs derived from geometric patterns, it is easy to see how they lend themselves to contemplative study as the elements of the patterns dissolve and reappear, all within patterns which can be understood to cover an infinite surface.
Geomancy
Distinct from sacred geometries is geomancy, a tradition of divination, but which has a tradition in the Arabic and other worlds with a relationship with numbers, not geometry. The divination is composed of two elements: numbers and a body of knowledge governing interpretation. The only reason I mention it here is that some believe there is a relationship between geomancy and mathematics and, by extension, astrology and cosmology to which sacred geometries, as I’ve mentioned, relate.
This is not just common to the Arabic world but has been pursued in many parts of the world and, in fact, still is. The Arabic form was called ’ilm al raml or sand science, and related to the making of sixteen random lines on the ground and their interpretation.
Decorative types

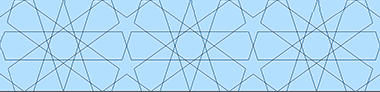
Studying the traditional buildings in Qatar encouraged me to look at the geometry behind them, particularly that associated with the patterns of naqsh, a significant element of the domestic architecture. While the traditional buildings of the peninsula and their decoration are relatively unsophisticated, the development of geometry in the Arabic and Islamic world is fascinating and is not confined to naqsh but also to wood, metal, tiles and a variety of other materials. This sketch, for instance, is of a wooden door from Egypt and is a pattern based on ten-point geometry, the three rosettes being simply joined to form a portion of a running band.
But the Arab world is responsible for many disciplines we now take for granted. In the sciences and arts they gave to the world considerable scholarship and, in their development of design, introduced the visual strength of geometric structure in their use of pattern.
These structures underly much if not all Islamic patterns, though sometimes this may not be immediately discernible or, more likely, not immediately spring to mind. One of the great achievements of Islamic design is the manner in which the geometries or underlying patterns are subservient and not immediately apparent.


The first two decorative examples to the side are from different areas of the Middle East and are separated by a hundred years. They are of floral or foliate designs which, while free flowing, have a very strong geometrical basis in the setting out of their pattern, and represent geometries enlivened by the cursive nature of the applied design.
You will see in the upper photograph, on a tile from the 1378 tomb of Buyanquli Khan of Uzbekistan, the use of two colours to bring definition to the design whereas, in the second photograph, of a 1277 Syrian marble bowl from an ablutions fountain, there is a single colour. Despite this, the complicated design is still legible. Note also that there is calligraphic script running round the basin just below its rim, though wear and tear has affected the top of it a little.

This third photograph is an example of calligraphic Arabic script, another of the Islamic arts that are applied as embellishments or integral elements of an Islamic design. In this example, a page from a Holy Quran, great skill has been used in the application of a set of rules to the creation of the page that has considerable meaning to both the artist and subsequent readers. While calligraphic, neither this nor the example below were constructed with single strokes of a pen. They are both artistically embellished.

The last of this group of photographs is of a plate from Eastern Iran or Uzbekistan, from around the tenth century, this time decorated with a highly stylised calligraphic phrase. Not only is there directional geometry centred on the plate, but the letterforms also have considerable attention paid to the geometry generating their individual and collective forms. At the bottom of the photograph you can glimpse part of a smaller plate where the outside rim is the baseline for the calligraphy whereas, in the larger plate, the baseline of the calligraphy is based on the centre of the plate.
The decoration of nearly all buildings and artefacts is based upon a combination of:
- Arabesque or cursive,
- calligraphic, and
- geometric or polygonal,
Calligraphy is not dealt with here as there are many resources on the Web as well, of course, elsewhere. I would recommend that anybody interested might visit the Islamicart and topleftpixel sites in the first instance. There are many other examples of calligraphic art which are worth looking at, such as this, dealing with novel developments of the art in an external setting. Here I will just look at the construction of natural geometries as these form the basis upon which artisans on site set out their designs and work.
This part of my writings has to do with Islamic geometry and design, but it is worth remembering that the geometries behind these designs pre-dated Islam. They appeared in many parts of the world, but it is likely that those originating in Mesopotamia were developed by many of the civilisations that followed in the region, spreading out from there with the advance of Islam.

Arabic geometry, at least the geometries I want to look at on this page, tend to have a significant degree of regularity in their use. At the foot of the page I deal with another form, though even that is based on regular elements. But it is interesting to see that, in Qatar, there are one or two examples of a new or developed geometric treatment which are worth noting. The Weill Cornell Medical College in Qatar has a number of interesting details in its architectural vocabulary. This walkway has a screen treatment which, while appearing to be irregular, will feel familiar to Arabs and those with experience of Arabic design culture. It seems a successful interpretation of traditional design both as a design motif and a signed route as well as a device to provide a small degree of protection from the sun.
A Western geometry
While this may not be the place to discuss Western geometries, it would be useful to illustrate something of the character of Western geometrical designs in order that it might be compared with the Arabic geometries being carried out around the same time. This is not intended to be anything more than a note on a single design.

This first illustration is part of the east window of an English cathedral photographed from inside the choir. It is easily recognisable as an element of a religious building and can be considered typical of this type of architectural detailing. Although much restored in the nineteenth century, this particular window was constructed, as were many others in England, in the fourteenth century and can be considered contemporary with many Islamic designs. What is significant, and the reason for its being shown here, is the difference in its constructional patterning, here based on six-point geometry.
Despite this there can be no doubt that while these features are a characteristic of Christian religious buildings, they owe something not just to their development from the Roman oculithat brought air and light into buildings, but to Islamic designs that would have been seen by travellers and those engaged on the Crusades.
It is not my intention to write notes about the conceptual issues underlying these designs but, in common with other similar constructions it should be borne in mind that they are considered to have a hierarchy of geometries relating to the
- visual form,
- symbolic meanings, and
- hidden structures or geometries.
The visual form consists of the interplay between the containing physical frameworks – usually the carved stone mouldings – together with the contained plain or coloured glass and the structural lead cames that are also design elements. In patterns such as these there is a three-dimensional character to the design which creates additional interest to the two-dimensional form.
Symbolic meanings are common to many of the art forms associated with religions. Numbers, colours and shapes play a significant part in these windows relating them to a variety of concepts, natural and supernatural elements as well as a variety of religious constructs and resonances. Much has been published on these issues and it is not my intention to repeat them here, but they are thought to inform a considerable range of designs all over the world and can give added levels for contemplation in those understanding them and, perhaps, those who might not.
The hidden structure or geometry is that which is mostly the subject of these notes: it is the basic geometry on which the different shapes are established and set out in relationship to each other.


Looking solely at the rosette at the top of the window, you can see that it contains three round trefoil rosettes alternating with three pointed trefoil rosettes. The round trefoils shown here are termed as lying, the pointed trefoils as standing. This first sketch illustrates the construction lines for a simple lying trefoil and can be made with only a pair of compasses set at the same radius and created around a central circle.
The illustration below it illustrates the way in which a standing pointed trefoil may also be constructed. What is evident with these simple constructions is that there are a number of choices that can be made when setting out the circles that underlie the the shape of the trefoil. Generally their centres are always located on the junction of two circles but may also lie on lines that join centres of circles or that radiate from the centre of the central circle. These are not shown on the two sketches of the round and pointed trefoils.

This type of construction can be extended to form more complex forms such as quadrefoils and cinquefoils. Here the same basic construction has been developed in order to produce a shape with six pointed foils – a hexafoil or sexfoil. In this case a second series of circles have been drawn, their centres on the circumference of the central circle, and with a radius illustrated by the horizontal line on the top circle.
While the sketches above illustrate simple constructions, the medieval stonemasons varied their geometries by moving the centres of arcs to positions off the main construction lines. Significant variations can be formed this way, and it suggests that the manner in which this was calculated may have been based on empiric or non-rational rules.
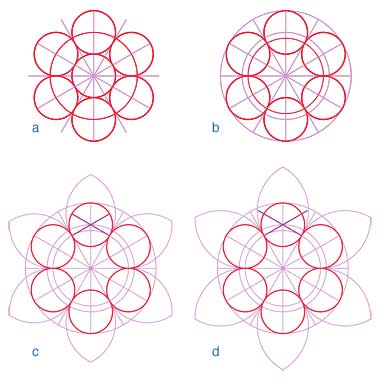
These four sketches are intended to illustrate how the centres for a pointed sexafoil can be constructed, and how its pattern can be varied by moving the centres of the arcs forming it.
In the first sketch, seven small circles are drawn that are mutually coincident, and six of whose centres fall along the circumference of a larger circle having twice the diameter of that of the small circles.
Where the outer six circles touch, a circle can be drawn passing through these points and having its centre at the centre of the central small circle.
Lines can be drawn from the points where this inner circle cuts the junction of pairs of the small circles and projected through the centre of the small circles.
In the third of these sketches above those lines are continued to meet the other side of the circle, making them the diameter of those circles. In the last of the sketches the line is projected further to a point representing a factor of 1.15 of the diameter of the circle, a point that does not fall on any construction line. From these two points, arcs can be drawn having their radii from those points to the junction of the two circles, and creating the shape of the sexfoil.
Note the difference between the two bottom sexfoils shown above – and here extracted for simplicity – where the establishing arc centres are 1.0 and 1.15 respectively but where, due to the necessities of its construction, the inner diameter of the foils remains the same. Obviously, the longer the line extends the greater the diameter of the sexfoil will be, and the flatter the shape of each of the foils.
In most of their respects, the geometry of these shapes are common to both Arabic and Western geometries and the designs produced from them, though the materials commonly used to form them might differ. As the geometries are so simple, this is not really a surprise. However, the method of determining centres outside the lines of geometry seems to be more common to medieval Europe.

Returning to the eastern window of the cathedral above, it is evident that the layout is very different in concept from an Arabic design, the geometry combining several different radii in order to produce what appears to be regular shapes, particularly in the six lines that radiate from the centre of the rosette, establishing the alternate round and pointed trefoil rosettes. To some extent this is due to the manner in which the masons set up the three-dimensional stone mullions. Note how, in this photograph, the heads of the adjacent pointed arches meet the ring describing the central rose.
One of the considerations of the masons was that the windows present very different effects when seen from the outside and the inside. The outside emphasises the two- and three-dimensional forms of the stone structure while, from the inside, the coloured glass is the main feature – though at night there will be a similar effect to that of viewing from the outside when there is no light behind the glass to illuminate it. Compare this photograph with that at the head of this section.

Here, then, is an illustration setting out the construction lines behind the central feature of the cathedral window. This is what is referred to above as the hidden geometry, though in blue I have emphasised the six trefoils. This may not be as accurate a representation of the layout of the window as I would like, but it is sufficient to see how this compares with the patterns illustrated on this and the other Arabic geometry page. In particular, you will notice that the majority of the Arabic patterns are running patterns; they extend beyond the frame in which they exist. This is a characteristic that has much to do with contemplation in Islam. Here the frame contains the pattern and this is a common feature of such Western geometries. The window forms a focus for those in the body of the church; it is a different form of contemplation that has much to do with the structure and hierarchy of the Church, and the sense of awe or wonder these buildings were designed to induce in their congregation.
The Winchester Palace rose window

As was demonstrated in the study above, the geometry used in many of the religious buildings in the West was often similar to, but different from those used in Islamic designs. This photograph is of the rose window in the ruined Winchester Palace situated on the south bank of the Thames in Southwark, London. Although suffering the ravages of time it is possible to see that it was based on six-pointed geometry, but organised with parts of its mullions crossing at points a little way from the perimeter.

The geometry is relatively easy to establish. The basic setting out of the hexagon within the circle is made by rotating arcs of the same radius of the circle around its circumference. The centres of each of the sides of the hexagon are determined by whatever method is most convenient and then two lines are drawn through those points at 60° to each side of the hexagon, and extended through opposite sides of the hexagon to intersect with the circle. The residual part of the pattern – that between the circumference of the circle and the hexagon – is one of the main characteristics of this type of Western geometry. It creates, as can be seen in the accompanying photograph above, and marked blue in this study, a very small and awkward area for design treatment.
The other characteristic of this type of pattern is that the centre of the pattern has broken away from the surrounding line elements with twelve unequal divisions that have been found at the intersections of the original arcs dividing the circle and the internal hexagon. This creates divisions from the centre of the circle of angles alternating between 25° and 35° – each pair subtending 60° from the centre of the circle – and none of them being a continuation of the main design lines joining the outer and inner hexagons.
Geometric design

My interest in the geometry of Arabic patterns began in the early 1970s when I first began to look at the carved naqsh plaster work that is a feature of the traditional architecture of Qatar. Most of those studies are no longer with me, nor are the finished works, some of which are in private hands. However, a few of the studies were photographed and although the quality is not very good, I have made a small collection of them into this animation in order to have a record as well as to show something of the way these patterns can vary. They were drawn on A4 sized paper using Radiograph pens. The studies did not all relate to naqsh but moved onto the more complex patterns found on panelwork, mainly Egyptian. The animation is not organised in any logical manner but is here solely for the purpose of illustrating some of the complexity of geometric patterns.
Returning to Arabic geometry, I’d like to begin with some notes on geometric design. This is a vast subject and better covered in many other studies. So here I would just like to introduce the concept of differences in pattern geometry.

The first thing to bear in mind is that the patterns with which designs are created are simple to construct, however complex some of them may at first seem. Here is an illustration of how lines can be formed that will provide, by selection, the framework for a pattern. It is deliberately complex in order to show how simple a concept can result in a wide range of guides for a designer to use in developing a pattern.
Starting from a single point, a line or circle can be constructed from which more lines and circles may be defined that create logical intersections with the original lines and circles, these forming points that may be selected for the development of a pattern. In this simplistic animation I have drawn a circle upon which twelve similarly sized circles move around its circumference. From the twelve points defined by their mutual intersections, lines are drawn to each of the other points. From there a number of other intersections are selected and have more lines added, joining them, and introducing a variety of angles from the general 15°, 30° and 60° angles associated with twelve-point geometry.

Purely as a notional illustration, here is a graphic showing some of the lines developed in the animation above, extended to form the basis for a larger design. This is solely an indication of how an infinite pattern might be established on the basis of the repetition of the simple twelve-point geometry developed above. Even at this scale where the detail is unreadable, the impact of the pattern is readily discernible and would be better appreciated in a design that did not use all the guidelines shown here.

While the animation above is based on overlapping rosettes, this pair of illustrations shows their simplest variations when organised for the creation of an infinite pattern based on a line of contiguously organised rosettes.
The first illustration shows how the rosettes are moved directly horizontally and vertically while, in the second illustration, they are moved horizontally and down at 60° to the original line. In the first case each rosette touches four others and, in the second example, each rosette touches six others.
There is no other way in which the rosettes can be organised contiguously without their being overlapped, as they are in the animation above.
A little more is written about the alternative ways of developing repetitive twelve-point patterns further down the page.
But here we should return to simpler construction. Below, I have set out ways of drawing each of the basic geometries along with some simply developed patterns for illustration.
To begin with, here are the two simplest geometric constructions that form the basis for many of the patterns to be found in Islamic decoration. They are respectively the constructions for six and four point geometries. You may find the methods slightly different from the constructions shown further down, but they all produce the correct results. These next two diagrams read left to right.
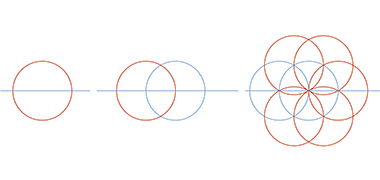
The construction of six point geometry is by far the simplest construction. Draw a straight line and, with the centre of your compasses on the line, draw a circle. With the compasses centred on one of the two points where the circle cuts the line, draw another circle of the same radius. With the compasses centred at one of the two points where this circle cuts the first circle, draw the next circle, continuing this process until there are six circles mutually intersecting and centred on the original circle. You will now have a basic construction for patterns derived from six-point geometry.

The construction of four point geometry is only marginally more complicated. Again, draw a straight line and, with the centre of your compasses on the line, draw a circle. With the compasses centred on one of the two points where the circle cuts the line, draw another circle of the same radius. Repeat this with the compasses centred at the other point where the first circle cuts the line. You will now have three circles, all centred on the line. With the compasses centred on the two points where the first circle cuts the line and the compasses set at a greater distance than the radius of the first circles, describe two arcs from each of these two centres above and below the line. Where these arcs intersect, draw a line. This will intersect with the first line at right angles. With the compasses centred on the two points where this vertical line intersects the first circle, draw two circles with the same radius as the previous three circles. You will now have a basic construction for patterns derived from four-point geometry.

These relatively simple geometrical constructions are easy to develop for pattern making. With a pair of compasses and a straight edge it is easy to create the circular forms and then, by joining various intersections, to produce the basis for a variety of pattern making. The points selected may be the obvious intersections or, as illustrated lower in the page, more unusually related points. These diagrams show the simplest connections.

In this first exercise I have taken the basic seven-circle rose from the six-point geometry construction illustrated above and shown how the basic pattern lines evolve. The first illustration shows, on the left, the basic circle rose with, to the right, the addition of lines joining the intersections of the surrounding circles with the basic circle to create a regular hexagon.
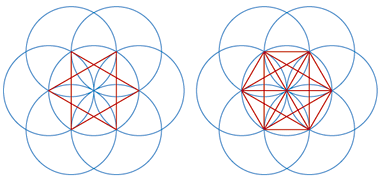
These two illustrations show how this simple exercise can be extended. On the left every second point of intersection of the surrounding circles with the basic circle has been connected, creating two interlocking, regular isosceles triangles, creating a regular six-pointed star. To the right it has been amalgamated with the hexagon to produce a basic pattern former that is found in many examples of patterning.

In this pair of illustrations the basic six-point geometry has been developed to form a basis for twelve-point patterns. Firstly, every second pair of the points of intersection of the surrounding circles with the basic circle, are joined as in the isosceles triangles example above, and then the points of the triangles’ mutual intersection are joined and extended to cut the basic circle.
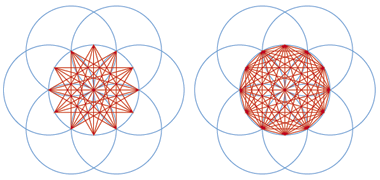
In the example above right, every fifth point on the central circle has been connected with what is, in effect, a continuous line to create a twelve-pointed star. In this pair of illustrations, that on the left has had added to it lines joining every fourth point to create a more complex pattern and, to the right, every point has been linked to create the most complex pattern.

Here is a detail of the above right illustration which gives more of an indication of the complexity of the underlying geometrical web formed by the development of the circular patterns. Looking at it you will see that there are natural junctions formed by the lines. This gives a series of points that can be used in the development of patterns. This type of framework forms the driving geometry for the relatively simple Islamic patterns with which we are familiar.

While there can be seen to be considerable room for variation in the dividing of a single circle, the more common basis for a pattern is a simple grid, here the development of the circle suited to six-point geometrical patterning. Even at this scale the eye finds it difficult to rest, but is continually moving around the circles. The addition of straight lines just develops and guides this movement.

Here, for comparison, is a basic grid based on the four point geometry illustrated above. Note that the circles in these two diagrams are the same size, but the patterns have markedly different visual densities. I have not gone through the exercise to demonstrate how the four-point geometry is developed as I have with the six-point above. But it will be obvious how squares, octagons and eight and sixteen point stars can be readily developed.
Axehead designs

Related to the above grid is the one shown here. This geometric grid is often used as the basis for a simple infinite pattern referred to as an al faas – an axehead or hammerhead design. One example of its incorportion into a piece of decoration can be clearly seen in the detail photograph immediately below illustrating part of a modern tile executed with fine craftmanship using materials with a strong colour contrast. A related design is illustrated a little way below.

The construction of these geometries is easily established with only simple tools. The basic geometry of the pattern above was created by moving circles one radius length apart, both horizontally and vertically to form the underlying grid. In the case of the lower pattern, the establishing grid is made on the diagonal, and rows of circles, touching on their circumferences, are located on those diagonals, alternative rows slipping by one radius with respect to the next.

The pattern is very common and can be seen all over the Islamic world as well as other parts of the world in both of which many commercial products have been produced on its geometrical basis. Here is an example of its use as paving in front of a hotel in Qatar, the basic pavior being enlivened by traditional Islamic decoration which has the effect of creating a texture to the otherwise simple shape. In this sense it can be compared with the pattern above where the use of shells creates the secondary interest.
The pattern is developed from a grid of circles, the first stage being to eliminate the lower half of each circle. Each alternate half circle is then rotated about the horizontal axis of its diameter and linked to its adjacent half circle to create a continuous wavy line. Each vertically alternate wavy line is then rotated about its central horizontal axis. A copy of the whole of this pattern is then rotated through 90° creating the basic pattern.

Closely related to the axehead pattern above is this slightly more complicated construction. Again, the basic setting out has not been given as it is created simply by the stacking of equally sized circles immediately adjacent, above and below each other to create the grid for a range of infinitely repeating patterns. Just a single pattern is shown in this illustration but it is possible to see the relationship between this grid with the photograph immediately above.

The axehead design shown above has a close relationship with a particular Moroccan design, which is illustrated below. Shown here is an intermediate design relating to its construction.
On a base of a grid of squares, a series of semi-circles are drawn, their diameters coincident with the vertical sides of the squares and being alternately mirrored moving along each vertical line. This creates a nest of similar shapes which can be used to cover an infinite two-dimensional area in a similar manner to the axehead design above.
Related to this design, as well as to the Moroccan design described below, this design is easy to construct and can be varied by increasing the relative size of the square to the semicircle.

This development of the basic pattern is developed from the square and semi-circles shown above. Here, the semi-circles are moved away from the square by a distance created by enlarging the original square by a proportion of 3:5. This automatically creates the square shoulders of the basic new design. Moving the new design away from the base design by 45° to a position equidistant between two adjacent designs creates an overlap. This allows a new design to be created, the overall pattern being created from the combination of the two designs.

This pattern has been placed here for the similarity of the character of its pattern with that illustrated above, but without the curves. The pattern is found as part of a screen in the development at Fatehpur Sikri, near Agra, Uttar Pradesh, India in an Indo-Muslim style, the development said to represent a fusion of local and foreign influences. The screens are carved from the local red sandstone and are comprised of a range of patterns. This particular panel illustrates a simple shape reflected and rotated in a similar manner to the axe-head designs above.

Returning to the first of the four-point patterns shown above, a slightly different development of this illustration is shown in the next diagram and is repeated here to show how a relatively simple pattern based on six-pointed geometry might be developed. The basic grid shown in the six-point study just above, has been turned 30° counter-clockwise and a number of straight construction lines selected on which the pattern has been produced. There are so many potential choices for the designer: this accounts for the great number of design variations that are possible.


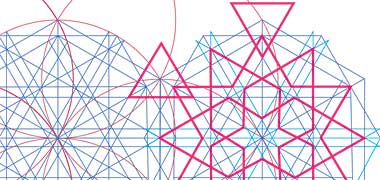
As I wrote previously, it is surprising how many variations can be made from a simple geometric shape. These first three illustrations show a pattern based on a study using six point geometry. The first diagram illustrates the basic construction, beginning on the left with the development from a circle of its basic, six point division; a simple exercise, easily made with only a pair of compasses. Moving towards the right, straight lines are added joining, at first, the intersections of the circles and, then, intersections of the straight lines with themselves. It is these selections which create the possibility for different patterns to evolve. In this first graphic I have shown an arbitrary pattern outlined in red as the result of this drawing and selection process. Incidentally, I have not shown all the creation lines for the small triangle which links the six-pointed stars, but on a larger scale it is easy to see how these are made.
The second graphic above shows how this geometric pattern develops when they are added together following the basic rules created by the selection process. The lowest of the three graphics illustrates how the decisions were taken to draw the straight lines on which the pattern is based. When I have the time I intend to develop this by illustrating different patterns created by varying the positioning of the straight lines.

As an illustration of how small changes can affect the overall pattern I have gone through the exercise again, this time I have organised a linear pattern more suited to tilework than to the more integrated pattern shown above.
The basic six-pointed star is arranged to touch at its horizontal and vertical points. As a six-point geometry produces an irregular appearance on the horizontal and vertical axes, then a different condition obtains when the stars touch horizontally and vertically. Note that I have made this a direct slide rather than move the stars across by half a unit. The second graphic illustrates the location of the straight lines on the pattern, the location of which can be seen to differ from those in the illustration above.

I have written more notes below relating to the types of pattern and how they are achieved. But here, as a demonstration of how different patterns can be produced by simple changes, I have taken the pattern above and moved each line of stars half way across and up to give a very different feeling, even though the basic star – and the horizontal line of stars – are exactly the same.

Here is just one more example. As a development of the preceding pattern, this pattern has been constructed with the same six-pointed star, but this time I have rotated copies around it through 60° instead of moving them 90° to the original star. Again it is possible to see how a very small difference can produce a dramatically different overall pattern.
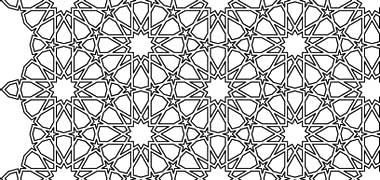

There are an infinite number of ways in which Islamic geometries can be organised to form patterns, as these notes may demonstrate. These two illustrations show yet another pair of patterns, their construction being readily understood, the top one based on dodecagons and triangles, the lower on octagons and squares. This page is not a scientific approach intended to display a rational grouping or progression of patterns. There are many other sites which deal with the way in which these patterns come together, particularly with explanations of the mathematics underlying them. The purpose of this small excursion has been to demonstrate how small variations of a simple two-dimensional geometry produce very different patterns. I have, however, written more about the seventeen different forms of pattern below using a simple form to demonstrate the differences between them, and the way in which basic shapes may be used.

Here is another design exercise created in a similar way to many of the geometries illustrated on these pages. In this case the underlying geometry is the simple octagon. Here the pattern is shown, but not all of the construction lines have been given as they can be assumed from similar layouts. The basic design consists of thirteen similar octagonal rosettes – one in the centre, four in the corners and eight surrounding the central rosette.
The central octagon was first constructed with lines connecting all its corners and then projected outwards in order to help establish the positions of the other twelve octagons. The central octagon can be seen to sit within a square set, in this example, at 22.5° to the vertical. The surrounding eight octagons also sit within squares that, together with the lines first extended from the central octagon, locate their positions relative to it.

As a development of this pattern, here is the beginnings of a running design that has been created from the larger pattern immediately above. Note that the junction of the pairs of large rosettes are not symmetrical about their vertical alignment, permitting a small degree of variation if the pattern is to be carried along. As with the larger pattern above, this design has been given a small amount of shadow in order to enliven the design, illustrating something of the richness to which the design lends itself.
A toroidal design

And now for something a little different. This pattern, or something very similar, caught my attention as it appeared to be a design that might be Islamic in character or at least in its construction – but which had a very different appearance from most of the Islamic designs shown on these pages. However, upon closer examination it seemed that there were construction lines that might be illogical, and it appeared that these might be readily amended to create a more logical design.
The finished rosette, which gives the impression of representing a twisted toroid, appears to be based on a simple hexagon. While there is certainly a hexagonal base, it can be seen from the finished design that its periphery is twelve-sided with the length of the sides alternating in the ratio of two to one.

The starting construction for the rosette can be seen on another page which illustrates how the side of a hexagon can be divided into three equal parts. That construction is developed, and various points are connected by lines with parts of those lines selected in order that the pattern can be effected using squares and two different parallelograms – with the smaller internal angles of 30° and 60° – all with the same length of side. Shading gives something of a three-dimensional character to the design, implying a toroid. This illustration shows all the lines that might be drawn from the geometry described above, many of them redundant at least over a part of the line. The points joined to create the toroid are not the obvious ones and need to be decided upon by inspection. It is an interesting exercise in developing a pattern.

The rosette developed above gives the appearance of being a toroidal three-dimensional object having an anti-clockwise twist to it – even when it lacks the notional shading given in the final stage. Logically the toroid or rosette can be mirrored to create an object with an apparently clockwise direction to it.
It is possible to join these two patterns together in a number of ways to develop an infinite pattern, though there will always be a space left at their junctions. This illustration suggests nine of the ways in which the clockwise and anti-clockwise patterns might be combined to show the relationships to be found in the creation of an infinite pattern.
A pattern based on squares

This photograph was taken of a grid of tiles and is here because, like many tile layouts, it is relatively easy to construct, compared with some of the complex designs developed for wooden panels and the like. Its attraction lies in the disposition of its squares and parallelograms, the two squares having their sides in the same relative proportions as the adjacent sides of the parallelogram, that is 2:√2, or 1:0.7071.

The construction of the pattern is illustrated in this animation. Start by drawing a horizontal line and, with compasses centred on the line, describe a circle. At the points where it cuts the line, continue to draw circles centred at those intersections and with the same radius. With compasses set to a larger radius, draw arcs above and below the line from points at the same positions as the original circles. These will intersect with the original circles. Next, develop a diagonal grid at 45° by drawing lines through the points of intersection of the vertical lines and circles. Add horizontal lines at the junctions of the diagonal grid and this will create the basic grid on which the design if organised. The pattern is then created by filling in the appropriate squares and parallelograms, .

In this exercise I have added, first, squares whose sides are the diameter of the initial circles. Then the smaller squares have been added, one group in the centres of the larger squares, the other group joining the top right and bottom left corners of the large squares. The residual spaces, the parallelograms, are given another colour and can be read as either trimming the large squares, or acting as spinning devices centred on a small square. Here is a larger section of the pattern which, in common with many Islamic designs, has the quality of being capable of reading in many different ways, the eye moving from one group of patterns to another, but finding it difficult to see more than one at a time. Even the progression of the smaller diagonally oriented squares have an illusory quality to them. Compare this constructed example with the original photograph above and note how the slightly different coloured small squares, located on a random basis, bring a significant amount of life to the pattern.
In a slightly different arrangement from the eight-point geometry above, the illustrative sketch below has been assembled in order to illustrate the way in which geometric designs may be assembled. In this example I have not included the construction lines for the guideline geometry in order to simplify the graphic. The importance lies in the selection of the points that are joined in order to set out, first, the central rosette, then the linking elements and, from those, the positioning of the next placement of rosettes that surround the first one.

The circle can be the most important element in establishing the basic placement of squares, as well as in determining the location of the sets of parallel lines adjacent to the centre of the circle that will form the central rosette of this particular pattern. First two squares are drawn at 45° to each other, centred on the circle and their sides tangent to it.
The spacing of the pairs of parallel lines is set by joining and extending the first pair through both adjacent corners of the two squares. Next and, in this case unnecessary to establishing the widths of the final pattern, the diagonals of the two squares have been drawn. Now draw pairs of parallel lines each side of the centre of the circle, their positions found by linking and extending the points where the two squares intersect. This establishes the central octagonal rosette.
With centres on the corners of the larger squares, circles are described with a radius set to the points where the smaller squares meet, respectively, the horizontal and vertical lines drawn through the centre of the first circle. With a centre on the point where these second circles meet the horizontal line, a third, smaller, circle is drawn which intersects with the horizontal line as well as the extended lines of the larger squares. These intersections create the octagon which establishes the distance between the first rosette and those that are located around it.
A pattern based on six-point geometry

This pattern, created as a panel in the Omar mosque, Jerusalem, has been included as it presents a slightly different character from many of patterns described on these geometry pages. Based on six-point geometry it appears to be constructed of broad strips of pattern that have been established at 60° to each other. This produces an infinite hexagonal pattern that can be read at a variety of scales. But while the centres of the strips of pattern can be seen to fall on the circumference and three diagonals corners of a large hexagon, establishing the widths of the strips is not as readily apparent because the guidelines tend to fall on minor elements of the basic geometry.

This animation illustrates the panel with guidelines indicating how the broad patterned strips might have been established. It is clear that the small central six-pointed star is the governing element of the design, and that it is from the internal junctions of the star that the guidelines are developed parallel with the sides of the large hexagon contained within the main circle. The same broad guidelines for the strips of pattern are used to link all the circles, so producing the basis for the infinite pattern.
But the setting out of the smaller elements of the pattern is a far more complex arrangement. Generally it is based on minor junctions of the underlying geometry, and it is interesting to speculate on why the designer took this route to establish the pattern rather than find a pattern using the more usual points of intersection. Undoubtedly the resulting pattern is interesting to the viewer, not just because of the banding effect, but perhaps more so because of the brain’s need to discover something of the underlying geometry of the pattern. This graphic illustrates most of the construction lines discovered in investigating the construction of the pattern, illustrating something of their complexity.

Here is the finished drawing of the pattern. It has a slightly different flavour in its application here compared with the original above but, as far as I can tell, is an accurate copy of the geometry behind the panel. It has been an interesting pattern to investigate due to the manner in which the selections of the pattern have been made, and for that it is a significant addition to those illustrated here.
The development of a rosette pattern

But there are many other ways in which patterns based on the square can be evolved. Here is basic framework that has been developed by rotating a square through 22.5° – one-sixteenth of 360°. The construction of the square, and the organisation for rotating elements of the framework, have not been shown in this illustration in order to keep it relatively clear. This is not meant to be used for a repeat pattern, but is a single rosette.
The outer heptadecagon, a sixteen sided figure, has been created by rotating a square – the outer square here – three times. If each of its corners is joined to the sixth neighbour, a number of smaller squares are created, their sides in the proportion of 0.7654 to 1.1414 with respect to the outer squares.
This exercise can be continued with successively smaller squares developed in the same proportion to their neighbours in order to create nesting patterns. But this only creates the basic framework from which a pattern may be developed; it is from the further linking of the intersections of these lines that a variety of patterns will be produced.
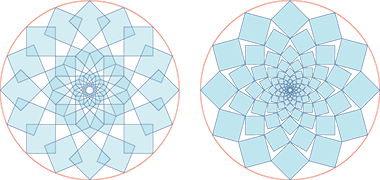
The rosette created above has some limitations when used in this way due to the overlapping of squares. This compares with designs created using twelve-point geometry where there is no overlap. A more fully developed illustration is shown below but here is a small scale comparison of a sixteen-point design on the left and a twelve-point design on the right. While the twelve-point construction demonstrates a spiral design, the sixteen-point construction develops squares in a reducing proportion along their diagonal, an effect looked at a little way below this note.

This illustration shows the result of a pair of simplistic exercises when more of the points of the original intersections are joined together, based on the illustration above. The results might be thought bewildering, the second perhaps more so than the first. Neither contain all the possible linkages but these two illustrations were placed here in order to get a feel for the possibilities in this geometry.
The two illustrations were both made as exploratory exercises looking at the ways in which a satisfactory pattern might be developed, but there are sketches that include even more complex lines that expand the simplicity of the original squares above and that are too dense to add to this scale of illustration.

The point to be made is that the designer is free to investigate and then make a selection from a variety of the possible points of intersection, developing a pattern from the choices made. Of course, at the back of the mind there must be a design idea for the character of pattern required and, from that idea the connection of points can be studied with a view to realising the original concept.
In reality this is a complex activity requiring considerable effort in looking at alternative variations that will lead towards the final design. In the course of the study, decisions can be made and changed at will but, as is evident here, the end design is not always the result that was anticipated and may end up being discarded.
This last of the above illustrations is the second attempt at producing a competent design, but it is still not the finished design I had anticipated. It was meant to have accuracy and a geometrical coherence, but on close inspection it continues to require considerable re-working to get it to a stage when I would be pleased with it as there are both conceptual and drafting errors that weaken the design and are disappointing. Some of the drawing errors are small and have been corrected, but the sketch is placed here as a record of a process and, hopefully in due course, will be replaced by a better design, or at least by a more accurate one…
Reducing squares in the proportion of 3:1

This animated graphic illustrates, albeit in too fine detail to be clear at all levels, the setting out of all the lines required to establish the squares at their different sizes, and is a development of the diagram above which shows the construction of a rosette. As with most patterns of this type, the lines join, initially, the external eight points of the design, with additional lines linking selected intersections of those lines.
One of the characteristics to note is the constant relationship that exists between adjacent squares as they descend in size moving towards the centre of the graphic. This is a constant, the areas of any two adjacent squares being in the ratio of 3:1, giving the ratio between the sides of two adjacent squares in the proportion of √3:1.
The animation above shows the squares reducing in size, their construction being created by the lines linking the octagonal frame as described. But the proportions of the adjacent squares can be established by this animation.

First draw a horizontal line and raise a square above it – obviously not all the construction lines are shown here but must be assumed. Measure or construct another equal square adjacent to it and, with the centre on the top left corner of the first square draw an arc from the top right corner of the second square to cut the initial horizontal line. Construct a square below the horizontal line with its side the length between that point and the bottom left hand corner of the first square. This square will be in the proportion of 3:1 with the first square. The line which is drawn from the top left hand corner of the first square to the top left hand corner of the second, larger square will create a triangle with the sides in the proportion 1:√3:2.
The above construction establishes the larger square beginning with the smaller square. Here is a construction that will establish the smaller square beginning with the larger square – the squares being in the same proportions as those above, 3:1 in area and with sides in the ratio of √3:1.

As with the construction above, first draw a horizontal line and raise a square above it. This will be the larger square. With its centre on the bottom left hand corner of the square describe an arc of arbitrary length which will intersect with the horizontal line some way to the right of the square. At that point of intersection, and with the same radius, draw an arc that intersects with the previous arc. From the two points of intersection – that, and the intersection of the arc with the horizontal line, draw two arcs of smaller but equal radius which will intersect.
From the bottom left hand corner of the square draw a line which meets this point of intersection. This line will intersect with the right hand side of the square, the point of intersection to the corner of the large square giving the length of the side of the small square. With its centre on the right hand corner of the large square and radius given by the intersection with the larger square, draw an arc which will cut the horizontal line and extend below the right hand corner of the large square.
Extend a line vertically down from the right hand corner of the larger square to meet the last arc, and drop a line vertically from the point of intersection of the arc and horizontal line. This will give the left and right hand sides of the smaller square. The full, smaller square can now be drawn.
A pattern based on a hexagon

Hexagons are used as the basis for a wide variety of patterns, sometimes as the central figure of a wider, infinite pattern or, as shown in this example, as a figure which creates a design apparently sliding at a slight angle and, therefore, one which is not particularly suited to a regular pattern within a rigid frame. In this case, the hexagons overlap each other to create the curious geometry behind this design.

The pattern is not difficult to create, this diagram having a number of construction steps missing in order to simplify the process, but which are easy to understand and establish using only a compass and straight edge.
Begin by establishing horizontal and vertical lines which will meet at the point forming the centre of a circle. This is also the centre of the hexagon forming the container of the basic design unit, its long axis being vertical. This second graphic is intended to demonstrate in a simplistic manner the construction sequence. Note how the containing red hexagonal outline is not completely filled, showing how the design blocks overlap to create the overall design.

This final graphic illustrates the angle at which the basic unit moves across the plane in order to create the continuous pattern.
If we think of the base of any one of the small red triangles as being of two units, then its height will be √3 units. By simply counting the triangles it will be seen that the pattern repeats after dropping 1.5 triangle heights – three units – while moving across five triangle widths 5√3 units. From this it can be shown that the angle of descent is the angle whose tangent is 3/5√3 or ArcTan 3/5√3 degrees, the pattern moving approximately 10.03° and 19.19° as indicated here.
A pattern based on two octagons

The pattern shown here caught my attention because it is completely based on octagonal patterning, the original having been carried out with inlaid marble on the seventeenth century tomb of Itmad ud-Dawla, located beside the river at Agra, India. This illustration is a notional reworking of the original. While the resulting pattern is clear and apparently simple in its design, it is instructive to look at its construction in order to see how the designer has added a few small lines while omitting a number of others in order to produce the final design.
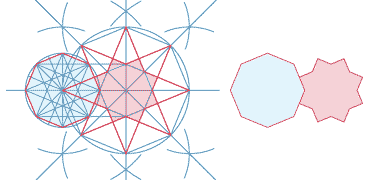
The design above depends on the creation of two eight-sided figures, one of them a regular octagon, the other a star-shaped octogon. On a horizontal base line erect a perpendicular and, from the junction of that and the horizontal line, produce two lines at 45°. From the common junction of these lines, draw a circle which will be intersected by the perpendicular and diagonals so that an octagon can be drawn along the circle. By joining the points of the octagon as illustrated in red, an octagonal star will be created. With compasses centred on one of the points of the red star and with a radius of its nearest internal point, describe a circle whose centre will fall on the initial horizontal line. An octagon can be created in a similar manner to the original, larger circle. Alternative construction lines have been added to this diagram in order to illustrate the relationship between the two octagons, shown here on the right. This pair of octagons are frequently found in Islamic designs.

In order to create the pattern shown above, it is necessary first to rotate the construction clockwise through 22.5° – an eighth of a circle – as is shown here. In addition, a number of lozenge shapes have been added as they occur naturally within the construction, forming an important element of the overall pattern. Their basic shape is determined by the natural connection lines established within the smaller of the two circles.

With the basic two octagonal shapes constructed above, the pattern can now be developed. This illustration shows the basic construction lines. Notice that the design relies upon there being a slight separation between the two groups of pattern, shown in this diagram as slightly different colours. This drawing apart of the design elements creates a space between the two elements, marked here by the blue circles, one each of the basic two octagons being shown in pale red and blue.
Here is the basic pattern with all the lines thickened and the spaces noted above filled by the joining of lines. The pattern created is interesting and would easily form the basis for a design in a variety of materials. While inspection of the pattern shows a series of octagons, lozenges and kite shapes, there are also some odd shapes created by the complexity of the design. So, the designer has omitted a number of the lines in order, it should be assumed, that a more clear pattern would be created as seen above.

With the basis of the pattern created above, the last illustration here is the same two-dimensional pattern as that at the head of this set above, though the outline colour has been changed, and a slightly different drawing style used with the intention of creating the appearance of an interweaving ribbon design effect, one which occurs in many of the examples of this kind of pattern work throughout the Arab and Islamic world.
A pattern based on nine-point geometry


Many of the Islamic patterns we see appear to have been established along simple geometric lines and, in a large number of cases such as the traditional patterns in Qatar, this is evidently the case. But we also know that designers have a wide range of decisions available to them when setting out the construction lines for any particular pattern. It appears that many designers will take the opportunity to develop patterns which seem uncomplicated and readily comprehensible, but which are not as simply organised as we might at think on first inspection. It is likely that Islamic designers see this as a positive feature of their work, adding to the interest inherent in complex geometries, and of benefit to those contemplating them, usually within the confines of a masjid where reflection is encouraged in the faithful.
This pattern is a case in point. The pattern is said to be of ceramic tiling at the Jaam’a masjid in Yadz, Iran, though I have not been able to find a photograph to support it. On first sight the pattern appears to be based on six point geometry, but although the setting out of the rosettes has been established on this geometry, the rosettes are created with nine-point geometry with the design accommodating or established on combining the two different geometries.
Elsewhere I have noted that it is not possible to make an accurate construction of nine-point geometry using the simple tools of compass and straight edge, though it is possible to make a decent approximation.
Examining designs such as this, which appear to be complex, my method is to open a copy in a drawing programme and look for obvious construction lines. When these appear to be evident then they are confirmed, or not, using a combination of geometry and trigonometry, preferably the former. It is important when constructing shapes within a drawing programme that angles and distances are established within the programme, and not determined by eye. The latter method tends to create errors which increase as patterns are expanded. In the case of this pattern, there were some surprising construction lines – though these could have been the result of my own inaccurate construction of the original pattern, of course.

When first looked at, the pattern seems to be based on hexagons, and it is anticipated that the rest of the pattern will be constructed that way. The left hand of these two details shows the basic setting out of the pattern in its hexagonal relationships. But while it might be anticipated that the group consisting of dark squares surrounding a triangle might be arranged symmetrically around a central nine-sided rosette, it is evident that they are not. In fact they are arranged in pairs only at the top of each rosette as is illustrated in the right hand details – here drawn to a larger scale. The result of this is that the relationship between a central rosette and the group of squares surrounding it, are not the same, making the construction slightly more unusual.

The left hand detail shows a basic arrangement of six groups, each of which comprises a nine-pointed rosette with a pair of devices consisting of three squares with their bases forming the sides of an equilateral triangle. The right hand detail shows six of these latter shapes and their relationships with the central rosette. It is evident that these shapes are not symmetrically arranged radially from the central rosette.
Instead they have been placed in what appears to be a simple pattern, the rosettes stacked in such a manner that they touch horizontally and vertically enabling the hexagonal pattern to become apparent. This graphic illustrates the pattern at its simplest with one each of the three shapes formed coloured for illustration.
The lowest of these three illustrations is here only to give an indication of the simplicity of the overall pattern, even though the construction of the pattern is far more complex requiring, as it does, a relatively complex or inaccurate method of construction for its nine-point geometry.
Establishing the setting out of the small group consisting of three squares and a triangle has been difficult. In fact I’m still not sure if this is correct, but at least there is a way of creating and locating the group which would have been available to the designer at the time and which appears to be relatively accurate. Like most works of this sort, the pattern relies on the joining of geometric points.
A line is extended left from a point on the top of the lowest nonagon. This establishes the base of the lowest square. From a point on the lowest nonagon a line is drawn to a point on the top of the higher nonagon. This forms the right side of the square. A line drawn horizontally between points on the pair of nonagons above the lowest nonagon will cut this last line. This establishes the length of the side of the square. This enables an equilaterally triangle to be established and the remaining two squares drawn on its sides. I have not yet checked mathematically, but it appears to be accurate enough for the purposes of the construction of this pattern.
more to be written…
A pattern based on ten-point geometry

This may seem a little different from many of the other illustrations placed on these pages. The photograph shows an example of a design created with ten-point geometry – but it is not Islamic. It is, in fact, a cast-iron manhole cover to a residential coal chute in a late Victorian terrace house in London. Around 300mm in diameter its interest to me lies in the creation of a little tension in the design by its not having the natural points of contact of the ten-pointed star meet any of the circles – either of the manhole cover or the inner and outer edges of its cast iron frame. By trial and error it appears to lie midway between them. Nor does the central circle have a relationship with the geometry. They seem curious decisions.

This simple animation illustrates the construction, though I have not shown the setting out of the basic ten-points as that is covered in other places. Firstly I have drawn the ten points on the circle which I believe is that which the designer established mid-way between the outer and inner rims of the cast iron frame. The ten-point star is comprised of two five-point stars interlocking. Next, at the internal intersections between those lines, a second group of ten points is created within the manhole lid. This produces a continuously delineated ten-point star. I have given some colour to the pattern, just to bring it out and illustrate how the points of the stars have been cut away. It’s an interesting design.
Exploration of a pattern based on ten-point geometry

The pattern that is illustrated here was developed from a ten-pointed star, but has some way to go before being considered a finished design. It is based on a cluster of ten, ten-pointed stars, and is shown on the left of these two illustrations. The geometrical construction of a single ten-point star has been covered on one of the other pages, so here on the right is shown only the basic divisions of a circle into ten parts, and the illustration developed to give one simple way in which the points of the star may be given a width related to the construction. The twenty-pointed star in the centre of the grouping on the left has been developed simply by extending the points of the surrounding ten-point stars, and adding a single shape between them.


The purpose of this exercise was to provide a design template that might be extended infinitely to cover a two-dimensional surface with some degree of simplicity. The start of this process was to look at a standard grouping that might be suitable for expansion, and that would not have interstitial spaces that were too large and that would require unusual or illogical geometric connections.
It was always evident that the development of the pattern would be difficult in that there are significant differences between six- and ten-pointed geometries which are hard to reconcile geometrically – though this is the problem that was interesting at the outset of the exercise.
Above right is an illustration of seven of the basic ten-point rosettes which have been arranged about their vertical axis symmetrically, and which have logical connections to each other. At first glance they appear to be a regular nesting set of seven hexagons, but the rosettes’ relationships on the diagonal can be seen to be very different from that on the vertical. Note that the arrangement of rosettes leaves six double-headed spaces between them which suggest that it might be possible to have lineal connections related to the shapes within the adjacent rosettes.
Turning the group anti-clockwise through an angle of around 30° produces, of course, exactly the same mutual arrangement, but a slightly more obvious illustration of the lack of symmetry there is about a vertical axis. Here are two similar orientations, but one showing three of the rosettes aligned horizontally, the second showing six small rosettes aligning vertically.

This graphic illustration is of four ways in which the above pattern might be oriented over a wider area. Because they have been left undeveloped or uncoloured, our eyes are drawn towards these double-headed spaces which give a strong indication of direction in what is exactly the same pattern – our comprehension of the pattern depending upon the position from which we view or experience it.

The double-headed spaces can be left unfilled if it is intended that the overall pattern might be more easily read. But filling in the double-headed spaces is not that difficult if we use similar rules or clues as to where the lines might connect and the shapes formed. There are two spaces to be filled as can be seen on this detail of the pattern – one large and one small. In fact the smaller shape is relatively small and its filling might even be omitted in a large use of the pattern.

Here construction lines have been set out based on intersections of adjacent elements of the ten-pointed rosettes. The resulting shapes that have been developed are a pair of pentagons on the larger space with a number of irregular hexagons in both the larger and smaller spaces. The latter have been given the darker colour, contrasting with their colour within the ten-sided rosettes, while the pentagons have the lighter colour. Experimenting, it was thought that, if this colouring was reversed, the pentagons would be too strong a design element within the overall pattern.
more to be written…
The development of a tricurve geometrical pattern

A correspondent has introduced me to a particular character of shape referred to as a tricurve triangle. There is much more to be learned about them and their geometries on two related sites, here and here, which are recommended for those with an interest in the mathematics behind the shape. The tricurve shape has a resonance in this example of tiling in the Alhambra, Spain which is looked at briefly further up the page, but is shown again here, illustrating its fluidity and capability for expansion as a two-directional pattern.
But there are obvious difficulties with using a shape that has curved sides with regard to fitting adjacent shapes. In the case of the tiles above, two hexagonal shapes have been used to fill between the curved shapes, though a circle would have been another possibility.

It is not possible to know how or when this shape may have been created, but the construction of the tricurve is a little more problematic than the shape above. In fact there are a number of these shapes that might be constructed and which are capable of being formed into contiguous patterns. This example creates a rosette with twelve points.
Although the division of a quadrant of a circle into three is not difficult, the mirroring of two segments is a little more so, particularly if carried out be an artisan. However it appears to be possible to come up with the tricurve using just a pair of compasses and straight edge as the next exploratory diagram illustrates.

This illustration is a little more ornate than is necessary, but was enjoyable to construct. With their centres upon a horizontal line, two concentric circles – one half the diameter of the other – are drawn and lines extended through their common centre to divide the circles into twelve equal parts at 30° to each other. The construction is not shown here. At the point of intersection of each of these lines with the inner circle, circles are drawn, each the diameter of the larger circle. Selecting a pair of circles, their centres defined here by the two small red circles, and adding the first, large circle, will create the three curved lines that will delineate a tricurve. The angles of the tricurve are 30°, 60° and 90°.

Taking the tricurve constructed above, this illustration rotates it about its smallest corner, 30°, to produce a rosette with twelve points. This in turn is surrounded with tricurves to form a continuous pattern. It can be seen that there is a rhythm in the manner in which the tricurve is located with regard to its neighbours, but the pattern has a central focus and does not lend itself to the production of a pattern that has no spaces between the tricurves.

However, it is possible to produce a pattern if the central grouping of twelve tricurves is used. In this illustration a combination of tricurve rosettes has created a pattern that appears to be regular, but has required adjacent rosettes to be placed clockwise and anti-clockwise in order to ensure that no rosettes obscure a neighbour. The resulting pattern can be seen to have a number of irregularly shaped spaces between the rosettes.

It is evident that there are a number of ways in which the tricurve can be used to form a pattern. In the first of these three illustrations an individual tricurve has been rotated around its second smallest angle, 60°, to create a six-pointed star. These nest comfortably together, but with there being two different residual spaces between any two tricurves.

This second pattern has been produced by using only six of the twelve-pointed rosette shown above, but with them all rotating in the same direction. Alternatively the pattern can be understood to be groups of three-pointed stars rotating in the opposite direction, these stars being created by joining three tricurves at their two larger corners, 90° and 60°.

Following a comment from a correspondent, this third graphic has been developed to illustrate a slightly different grouping and, further, how such a pattern might be fabricated using a small number of tiles. It can be seen to be similar to the pattern shown three illustrations above, but using more regularly shaped tiles. There are two pale blue tiles that would be used to construct the spinning stars shapes, one clockwise, the other anti-clockwise.
Shown here at a larger scale, it can be seen that the green and purple infill tiles are asymmetrical and are handed. The smaller blue infill tiles would be of two kinds, and rotated into place, the lighter blue tile being symmetrical about both its axes, whereas the darker blue tile is symmetrical only about its vertical axis.

The examples of tricurves above are all based on tricurves with 30°, 60° and 90° angles at each of their corners. However there are other possibilities such as tricurves with 36°, 72° and 72° angles. While the former tricurves are suited to six- and twelve-point patterns, the latter are developed into five- and ten-point patterns.
This animation illustrates one way in which the 36° 72° 72° might be constructed using only a straight edge and compasses. It may look a little complicated but that is because I have used the full construction of a pentagon in order to illustrate the development of the necessary angles, as well as showing only a limited number of stages of the development.
First establish two lines at right angles to each other and, with their meeting point as centre, describe a circle. On top of the circle draw a tangent to the circle. At the junction of the vertical line and tangent construct a pentagon with its right, lower corner at that junction.
The construction of a pentagon is shown in a little more detail on this page. Joining the bottom right corner of the pentagone with that opposite creates an angle of 36°. From that point a line can be constructed at right angles to the 36° line from which a circle can be drawn so that its circumference meets that line as a tangent. This circle and the original circle now establish the paths of two sides of the tricurve.
To complete the third side of hte tricurve it is necessary to construct another pentagon, this time with its middle left corner at the point of intersection of the original horizontal and vertical lines. From that point a line must be drawn bisecting the angle between the two lines within the pentagon connecting that point with the opposite two corners of the pentagon. That line will intersect the two large circles. From those two points describe arcs with the same radius as the two large circles and, from their point of intersection, draw the third large circle. This will establish the third side of the tricurve with internal angles of 36°, 72° and 72°.
For those with an interest in tricurves, there are notes looking at their geometry on three more related pages, here, here and here.
more to be written…
Construction of a basic twelve point geometrical pattern


The construction of a basic twelve-point geometrical pattern is relatively easy. The design shown here is one of many which can be extended to create a pattern with many variations dependent upon the intersections selected both within the design shown here, or in its connections with its repeats or with its interconnections with other designs.
Begin by drawing a horizontal line and, from its centre draw a circle and then raise a vertical to divide the circle into four segments.
Although the construction is not shown here, draw two hexagons contained within the circumference of the circle. The easiest way of doing this is by using intersecting circles of the same diameter of the original circle, their centres along its circumference.
By connecting every fourth intersection of the hexagons with the circle, a square can be constructed. Repeat this twice more to create a total of three squares.
At the intersections of the squares and hexagons, six pairs of parallel lines can be drawn establishing the width of the arms of the star. Alternative widths can be established, but this is a way of creating a basic twelve-pointed star.
This second illustration shows a small number of variations made by assembling six of the above design in slightly different hexagonal relationships with the central element. No attempt has been made to add or subtract links but it is evident that these might be readly made. Not only can infinite designs be made in this manner, but the elements can be moved further apart as shown in the last two of this illustration, as well as other lines added to create more complex infinite designs.
Alternative design guidelines developed on a twelve point circle

The number of ways in which the geometric patterns on these pages can be developed appear to be infinite. Well, perhaps not infinite for all cases, but they are certainly capable of forming the bases for a considerable number of different patterns. At their simplest, and for the majority of the basic patterns, there will be a circle whose circumference is divided by a number of points dependent upon the pattern required.

The first diagram, above, was started with three similar-sized circles divided into, respectively from the left, six, twelve and eighteen parts, and with all the points connected to each other to produce an increasingly complex basic pattern. As you would expect, the more points on the circumference, then the more possibilities there will be to create patterns formed only on those lines. A grid such as any of these would have been easily accomplished by anybody using compasses and straight edge and could be used to form rosettes with a variety of complexities. But while complexity can be seen to increase with the number of divisions – compare the divisions of the first diagram where each circle is a multiple of six – it can also increase by moving from even numbered to odd numbered geometries – the lower diagram compares circles divided into eighteen and nineteen, additionally allowing a slightly different character of geometry.

It is the selection of lines which creates the character of the eventual pattern. Although the basic geometry is the same, there is considerable variety possible in the resulting patterns. This animated diagram illustrates just a small number of the alternative patterns – in no logical sequence – which are capable of being formed by following different selections of the guidelines of the basic divided circle, in this case, the central circle of the three above, the circumference being divided into twelve parts.
Each of the individual diagrams has been constructed by creating a single shape based on the underlying geometry and rotating it about the centre of the circle in increments of either 30° or 60°. You will notice that some of the patterns have symmetry while some of them have implied direction or motion, this being dependent upon the selection of lines.

It should also be noted that there are no secondary lines joining intersections of the connection lines of the rosette – a common way of developing additional geometry upon which to create patterns, as is demonstrated here, the secondary lines being shown in red.
Where the basic shape is simple and has few points of division, the secondary lines tend to concentrate in the centre of the rosette, as can be seen in this example. As the divisions of the rosette increase, the secondary lines move towards the outer edge of the rosette, permitting a more complete pattern as opposed to one mainly suited to decorate the centre of the rosette.

This next pair of rosettes illustrate how the secondary guidelines create additional means for the elaboration of patterns. On the left is a six-pointed rosette, on the right an eight-pointed rosette showing how the central area of guidelines enlarges in this simple progression. On the six-pointed rosette there is also a third secondary series of guidelines created by adding lines between the intersections created with the secondary guidelines. I have not added the third secondary series to the eight-pointed rosette as it would be even more difficult to read than the six-pointed rosette, that being difficult enough at this scale.

The reason for selecting the particular geometry illustrated above as an example is that hexagons can be nested together easily and their construction lines readily joined to form continuous patterns as is illustrated in this example. It should be added that this is not a well-worked out example and could benefit considerably by rationalising a number of the elements. The light colouring suggests where the problem areas are. This ground pattern, for instance, has been created from one of the above patterns and simply repeated, their junctions automatically creating triangles and parallelograms between them.
These diagrams have been constructed so that some of them might be joined in this way, but there are also some which might be developed as frames and have additional patterns created within them, perhaps developed with the secondary systems described above. Perhaps these will be illustrated later…
Variations on a twelve point geometrical pattern

It is possible to develop twelve-pointed stars in a number of ways, the normal construction being developed from the design illustrated on the page showing the construction of a six-pointed design. The basic star can be considered as being formed from either three isosceles triangles or three squares rotated at 30° to each other, or two hexagons, again at 30° to each other.
Note that the dodecagon established with squares sits at 15° compared with those formed from triangles and hexagons.

Based on the notional constructions shown above, it is evident that there are many variations that might be developed when composing patterns that are based on twelve-point geometry.
This diagram illustrates that there are theoretically eleven points that might be joined by straight lines from each of the twelve points on the perimeter of a circle which has been divided into twelve equal sections – although obviously half of these are doubled, as they are the points directly opposite each other.
It can also be seen, from those marked in blue, that there are six groups of five and six parallel lines within those straight lines and which might be utilised in the development of patterns.
All these lines may be used as guides when patterns are being developed but, just as important, if not more so, their mutual intersections create points through which other lines may be drawn such as in the development of star patterns such as in the illustration that follows.

There can be many variations developing the patterns formed using twelve-point geometry. But one of the significant issues relating to star designs based on twelve-point geometry concerns the width of the arms of the twelve-pointed rosettes or stars, particularly when the sides of the arms are parallel.
In this graphic animation it can be seen that their width or thickness varies in the five examples given, producing different effects that make considerable variety in the aesthetic of the star and, by extension, to elements joining and relating to it in any expansion of the pattern. A similar argument obtains for stars whose arms are not parallel.
For the purpose of this illustration the widths of the arms has not been created by a development of the basic geometry – the star has been produced by rotating a hexagon through 60° – but by measuring the points at which adjacent edges of the arms meet. Arbitrarily they are shown for distances from the centre that are respectively 25%, 37.5%, 50%, 62.5% and 75% of the distance from the centre of the circle to its circumference.

Contrasting with the method suggested above, here is a more logical design based on lines which have been developed within the basic construction of the twelve-pointed geometry. This twelve-pointed star was produced in the process of constructing a pattern of contiguous twelve-pointed stars packed as close as possible – essentially the pattern is a hexagonal grid.
The construction of the basic circle and its subdivisioning into twelve points is easily developed with compasses and straight edge. Lines are then drawn from the twelve points on the circumference to every fourth point, essentially creating three squares rotated through 30° with respect to each other. A circle is described from the same centre as the original circle and meeting the sides of the squares at a tangent. The diameter of this circle is approximately 70% of the diameter of the original circle.
Lines are drawn from the intersection of that circle and, with these as guides, the basic pattern can be defined, comprising three different shapes surrounding a fourth, central star. Grouping more of the stars around the first star it will be seen that there are two more shapes defined, a narrow diamond and an irregular, but symmetrical hexagon.

Note that, for the stars to meet accurately, the describing circles will intersect and not meet at common tangents to each other. However, their positions are easy to locate, their centres being located at the intersections of six of the circles used to create the original twelve-pointed star – two of them indicated in this diagram by the two small light blue circles.

A second consequence of this accurate creation of pattern lines is that the angles of the pattern lines will have a common turning point. If the lines of the pattern have a significant width, then the lines of each rosette will overlap the lines of adjacent rosettes. For this reason careful consideration needs to be given to the way in which the lines are designed at their turning points and junctions.


By way of contrast, these two graphic illustrative details can be compared directly with the detail immediately above. In the first detail here the lines of the pattern have no width, leaving the individual pattern shapes and their colours defined and contiguous. In touching each other, the shapes rely on suitably selected contrast in tone and colour for their effect, something that is more difficult if there are no dividing lines. It is apparent that there is a very different effect when compared with the preceding illustration.
While something of this effect may be obtained by having stronger colour contrasts, a much cleaner effect is obtained by including bounding lines to separate the coloured shapes. Here, where a white bounding line is selected, a much more attractive design may be produced. This particular effect can be compared with the illustration at the beginning of the next note where the white line is wider, itself becoming a more important design element.

However, not only is the width of the dividing line important, so is its colour. While white allows the pattern colours to dominate the overall pattern, the use of colour in the bounding lines has a direct effect on our perception of the colours of the pattern, and needs to be carefully selected together with the colours of the pattern due to this effect, as can be seen in these six random coloured line examples.
A twelve point geometrical pattern

The development of patterns using simply available instruments, the compass and straight edge, must have been an interesting process. To what extent the development of mathematical concepts may have guided the early designers is impossible to judge. But it would have been feasible for a designer to come up with complex patterns without any or with little mathematical knowledge, only the fascination inherent in developing patterns by the joining of points and lines and, perhaps, the urge to create non-representational designs of beauty either as framed elements or as infinitely expandable patterns.
The pattern illustrated here may have come about by such a process. I have illustrated it here as a framed design suited to be used as a decorative panel, but the pattern is infinitely expandable as can be seen below. Although it may seem complicated because of the number of lines that I have developed, the principle is simple ― just draw lines that connect points of intersection starting with the simplest of outlines, the circle. Many of the lines are, in fact, unnecessary, but have been included as decoration having established points for the final pattern.
As with the drawing of most patterns it is necessary to start with a horizontal line upon which there is constructed a vertical line. I have not shown this construction. With its centre at their intersection, describe a circle and, at the intersections of the circle with the horizontal line, describe two more circles of the same radius followed by four more circles at the intersections of the first three circles, thus establishing a hexagon.

Connect each alternate point of the hexagon and, at the point where each of the two horizontal connecting lines intersects with the vertical line, draw a circle with its diameter set to the intersection of two of the large circles. With compasses at the intersection of the horizontal and vertical lines draw a small circle with its diameter established by the intersections of the last two circles and the vertical line. With compasses set to this diameter, draw twelve more circles. In effect this locates two rings of small circles set at the corners of two nested hexagons.
Draw lines connecting the alternate corners of the inner hexagon and then, at the points of intersection between the small circles and the lines connecting the alternate corners of the inner hexagon, draw lines that will complete a dodecagon. Now construct small squares linking the six inner hexagons and then add lines running through the centre of the pattern between opposite corners of the hexagon ― the horizontal line already links two of the corners.
The next lines are drawn between the intersections of the large circles and the small circles of the inner hexagon. Now draw lines between the intersections of the small square and the line describing the perimeter of the inner hexagon, and are then extended outwards.

Draw a series of hexagons, one in each of the small circles at the corners of the inner hexagon and, finally, draw and extend lines connecting alternate intersections of the inside edges of the small squares. You will now have the guide lines for the pattern. Actually, there will be a small number missing at the corners that I have left out, but that can be readily assumed by extending the underlying pattern. This graphic illustrates something of the character of the pattern when extended and can be compared with its design as a panel at the beginning of this note.
A twelve point spiral pattern


As with other geometries, twelve-point geometries can be developed into a wide variety of patterns, either as separate discrete designs or as continuous patterns that may be developed infinitely. Designs are often produced combining twelve-point geometry with other bases, increasing the visual complexity of the finished design.
In this particular example there is only twelve-point geometry used as a basis for the design. It is not a design that can be expanded as a pattern, though theoretically, it might be expanded to infinity moving out from its central point. A ring of twelve squares has been created, the squares reducing in size as they move inward, producing a spiral effect and creating a discrete design that appears to be readily expanded outward.
However, this design has been produced starting with a circle within which concentric rings of squares move inward towards the centre of the circle until the squares become too small to be seen effectively. This example was drawn at A4 size and contains eleven rings of squares, the study then being reduced for illustration here. Because of this there is an inevitable lack of detail towards the centre.
The design is developed starting with a ring of twelve small squares within and touching the circle. A second, smaller, ring of squares is then added, touching the first ring of squares. Note that the length of the diagonals of the second, smaller ring of squares is equal to the length of the side of the adjacent outside squares.

The mathematical relationship between the smaller and larger squares is interesting. In this illustration it can be seen that the length of the diagonal, CF, of the small square is equal to the lengths of the sides, CB and CD of the adjacent larger square which it touches at C – and forming an equilateral triangle, BCF, with the sides of the two larger adjacent squares.
By inspection or calculation it can be seen that the area of the larger square is twice that of the smaller square.
A twelve and six point geometrical pattern


This two-dimensional geometrical arrangement, a regular distribution of twelve point rosettes, should be familiar to most people as it can be found decorating a wide range of buildings and objects, with its construction being executed in a variety of simple or expensive materials, and at different scales.
Based on one of the simplest geometries to draw, the overall design is developed within a regular, infinite hexagonal lattice, the twelve-pointed rosettes being established at each point of juncture of the hexagonal grid.
However, the first image, together with those immediately below it, are really placeholders for a completed construction as I am not sure of the correct construction of the smaller elements of the pattern – those which are located between and around the main twelve-pointed rosettes, nor am I certain of the importance of accuracy with regard to the size of the inner circle.
Only their basic containing shapes, a square and regular hexagon, have been added in the first three images. It is entirely possible, if not probable, that there are a number of geometrically logical, alternative constructions possible, but what is shown here is an exercise aimed at establishing a simple way of setting out the whole of the pattern.
The second image shows a single grouping with a central rosette surrounded by six similar rosettes.
The third image shows just the top pair of the six rosettes that surround the central rosette, but with the constructions of the spaces between the rosettes still to be defined.
These smaller constructions are designed with six and eight points contained respectively within the hexagons and squares linking the rosettes.
A small six-pointed rosette is situated within the hexagon between each junction of three twelve-pointed rosettes, and there is also a small symmetrical octagon in the square located between each pair of twelve-pointed rosettes.
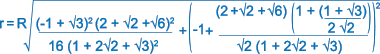
When this study was first embarked upon it was thought that the outer and inner circles of the circles used in the construction of a rosette had diameters in the proportion of 2:1. However, this is not the case, the diameter of the inner circle being very slightly larger at 0.5043144802900763 of the outer as established in this equation.
In order to design the first of the large rosettes, begin by drawing a circle and upon it construct a regular icositetragon – a twenty-four sided polygon – by using a straight edge and compasses stepping along the circumference of the circle set to the same diameter of that circle. The construction is not shown here but is readily developed from the construction of a hexagon.
From each of those points of contact of the icositetragon with the outer circle draw two lines to a pair of points on the opposite side of the circle. These lines will intersect with each other and, from the centre of the large circle, describe a smaller circle whose radius is that of the points of intersection of those lines. It will be found that this is very nearly a measure of half the diameter of the large circle – see the proof in the note two paragraphs above.
On the inner circle, construct a dodecagon – a twelve-sided polygon – and, with their corners at the centre of the faces of each side of the decagon, construct two hexagons inside the circle. Again, the construction is not shown here.
The central rosette can now be marked out, its lines defined by a combination of the the sides of the hexagons and the lines crossing the outer circle.
As mentioned above, the small containing square has an octagon sitting within it. In order to set it out, first the diagonals are drawn as well as lines across the square from the centre of each opposite side. Continuing the lines at the end of the adjacent rosettes to their junctions with the diagonals of the square enables the full construction of the octagon to be drawn.

Establishing the lines of the hexagon is a little more complex. This graphic aims to show in the simplest manner, the construction lines which will define the hexagonal rosette. The outer sides of the hexagonal rosette are created by following lines exending from the outer sides of the larger hexagonal rosettes on the three sides surrounding it. This produces a regular defined rosette, though it should be noted that there are similar patterns creating irregular petals to the rosette. Note that the five-pointed stars are all irregularly shaped.
This final animation illustrates a central rosette surrounded by six regularly distributed rosettes of the same size, with the space between them containing the small octagons and small hexagonal rosettes, their constructions illustrated in the two images immediately above.
The pattern can be directly compared with the second of the illustrations in this note, and be seen to have the squares and hexagonal spaces in that design now each containing octagons and six-pointed rosettes respectively.
Caveat artifex: while the above construction is believed to be correct there were a number of small errors recognised in setting out the construction, creating the possibility that the pattern may not be as accurate as it should be. However, at this scale, the pattern looks acceptable.
Finally it should be noted that there are constructions for the small, six-petalled rosettes which create regular rosettes within the square. This results in the outside lines of the petals not lining through with the outside lines of the larger, adjacent rosettes, perhaps creating a marginally more lively design.
A twelve and nine point geometrical pattern

As mentioned previously, these studies were begun years ago, premised on the belief that Islamic patterns were capable of construction using the simple tools of a pair of compasses and a straight edge. This particular pattern is found on the Tashkent scrolls, and this note is based on the investigative work carried out by Lynn Bodner, the reference being recommended viewing for a far more detailed description of its construction than is set out here.
The pattern is notable in that it is comprised of twelve, nine and five pointed polygons arranged in a continuing design. Most of the patterns I have set out on these pages have been established by using construction lines that create regularly shaped polygonal stars. This is different in that while the twelve-pointed star is regular, neither the nine or five pointed polygons are; both of them require slight distortions in order to sit into the pattern comfortably. At the scale of my illustration here, this is hardly noticeable though is very evident during the design construction process.
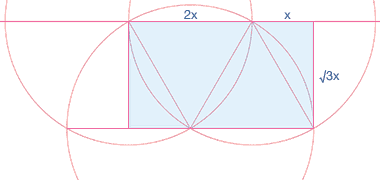
The basic rectangle within which the pattern is developed has sides in the ratio of 3:√3 due to its being formed from 1½ equilateral triangles ― an equilateral triangle having sides in the ratio of 2:√3 of its height.
This rectangle is created using interlocking circles to form the first two mutually coincident triangles, then extending their bases to create the longer horizontal sides and dropping verticals to create the shorter sides.
A link to the step-by-step construction is given above. This animation attempts to describe the general principles that are likely to have been taken by the original designers of the pattern.

Following the construction of the rectangle – the construction not being shown here – a diagonal is drawn between two of its corners and then six lines drawn from those corners, bisecting the angles formed between the diagonals and the sides of the rectangle and the two triangles.
Two circles are now drawn, their centres on opposite corners of the rectangle and with their common radius set at the intersection of the bisecting line and rectangle’s shorter side. Three of the twelve points of the dodecagons to be established along these two circles are set at the intersection of the circle with the three bisecting lines previously drawn.
The other points can be readily found by extending those lines across the two circles. The corners of the dodecagon are established by connecting the fourth points of intersection along the circumference of the circle.
Lines are drawn between the top of each of the original triangles to the intersections of the rectangle’s diagonal with the two circles, and with the intersection of the two circles with the shorter sides of the rectangle.
Two smaller circles are now drawn that will establish the corners of the two nonagons. The centres for the circles are at the top of the original triangles, and their radius is set to the point where the bisecting line between the shorter side of the rectangle and the side of the triangle cuts the longer side of the rectangle.
Extend the lines from within the rectangle that meet at the centres of the two circles through those centres to intersect with the far sides of the circles. This will establish the nine points of the nonagon. Connect every third point along the circumferences to create the two nine-pointed stars.
In order to begin the process of extending and adding the necessary, additional construction lines, now draw circles with their centres at the centres of the four original circles and their radii set to the intersections of the long edge of the rectangle and one of the bisecting lines – in the case of the smaller circles and, in the case of the larger circles, set to the intersection of one of the chords of the dodecagon with a line joining the centre of a smaller circle with its intersection of the rectangle’s diagonal with the larger circle.
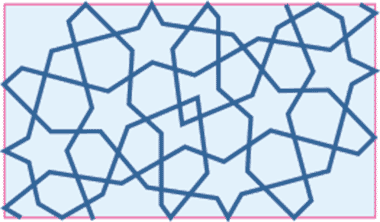
Extend the lines forming the corners of the nonagon and dodecagon to their intersection with the circles and, from these intersections, draw lines connecting the small and large circles. Part of this, latter, action will create points where the extended nonagons and dodecagons touch to create an element of the finished pattern.
Now, draw circles with their centres at the centres of the original circles, and their radii set to the point of contact described above. These circles will establish the points where lines may be added from the existing lines which, together with a small number of lines that can be determined by inspection, completing the underlying geometry of the pattern.
A twelve and fifteen point geometrical pattern
The sources mentioned above that deal with the ways in which geometries are brought together, tend not to help with the more artistic decisions that govern the designs of patterns. These can depend on a number of factors relating to traditions, the location of the finished work and the time available to design and execute the works. I have to admit that I have not seen a designer making one of these patterns other than artisan craftsmen in Iran and Qatar who were producing relatively simple designs, and who were able to explain something of what they believed governed their work. In those cases tradition was the main generator, together with a number of rules that governed what was – and what was not – permitted within that tradition and the designer’s understanding of the part the panels were to play in the overall design of the buildings in which they would be located. What is interesting is the degree of freedom they have to make design decisions. Yet a number of designs are evidently copies of other work and can be seen to be the continuation of traditional work in a newer context.

I have to admit to a fascination in the geometry behind such patterns that is as interesting to me as the patterns themselves. Here, for instance, is a working sketch behind a pattern that comprises a mixture of twelve-point and fifteen-point geometries. The basic elements of the geometry are far simpler than set out in this illustration, but I have added the more complete construction lines in order to make their underlying patterns more apparent. You should also be aware that the panel occupies only a small part of this pattern and, like many patterns, should be understood to be an infinite pattern of which a part has been selected for display. This is part of the charm or beauty of such designs. While the eye moves over them, there appears to be an understanding of their extending beyond the frame. This is one of the effects produce in the tilework and plasterwork of masaajid enabling the faithful to relax while immersing themselves in the infinite.
As you can see from many of the diagrams in this section, it is not difficult to construct a rosette with a variety of points on its compass. Generally rosettes can be constructed with a simple compass and straight edge, though it is evident that in many cases it would have been practical to operate with pre-cut formers that would establish shapes and relationships more rapidly. Rarely would a design be drawn from scratch although there may be be a need to experiment before establishing a final design.

However, when designs are complex it requires more than a set of formers, at least in the initial stages when there is a need to test potential designs and investigate the manner in which the patterns might best fit together. In particular, the designer must establish the points from which the overall setting out of the design are made. Conversely, when investigating the geometry of patterns, it is understanding this framework that is the analyser’s goal.
So, here is the basic setting out of the twelve-point rosettes for the pattern of rosettes illustrated above. The key generators in this layout are the circles, shown blue, of the same diameter as that in which the first, central, rosette is configured. These establish not only the positioning of the six rosettes that surround the central rosette, but also the centres on which the fifteen point rosettes will be constructed. In geometries of this sort there is a considerable degree of coincidence in the geometries relating each rosette to the others.

The construction of a twelve point rosette is shown elsewhere, but here is a detail of this particular rosette. Generally all these rosettes are constructed the same way: the circumference is divided into the required number of points and those points joined, each to all the others. The possibility also exists for lines to be drawn between the points of intersection of these lines, and that enables shapes such as the elongated lozenges, here shown in blue, to be drawn. Also shown in blue on the right is the circle construction that locates the centre of the three rosettes as is shown in the diagram above.
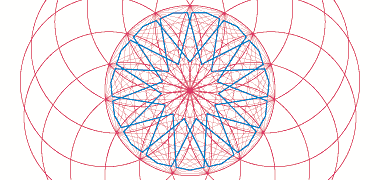
Here is a detail of the fifteen-point rosette. The greater the number of divisions of the circle, the more intersections there will be, and the more opportunities there are for establishing lozenges and other shapes on those points of intersection. In the case of odd numbered rosettes, it is not possible to construct the rosette as a single lozenge, rotated as you can see in the above illustration. In this case a continuous line creates the rosette giving the appearance of a number of rosettes, but not permitting the same kinds of treatment that even numbered rosettes allow the designer.

Although this note has to do with the construction of patterns, I have not shown all the construction lines for this part of the pattern, the extension or linking of the rosettes. Nevertheless, these lines are formed in a similar way to the rest of the pattern, by the extension of lines governing the rosettes. The skill of the designer lies in selecting the clearest elements to follow.

Here is the completed pattern as it appeared in an article a number of years ago relating the twelve and fifteen point geometries to a complex Saracenic pattern. There are many designs similar to it, some simpler, some more complex, but they all have a similar theoretical basis in their constructions; they rely on the skill of a designer to understand the underlying geometry of each rosette, and to develop and extend the controlling geometry along reciprocal lines, so linking them rationally and artistically. All the designs on the page will have been constructed in a similar manner, most of them less complicated than this.
There is a relatively small selection of design parameters within which the designer has very sophisticated decisions to make, most of them dependent upon the inherent geometric characteristics of the circle. The most important, perhaps, is the need to keep the design readily legible and comprehendible. Aesthetically, the more points on the circle, the more the design is likely to block up, or lack clarity due to the density of lines. In achieving this, one of the methods available to the designer is to increase the circle diameter as the number of points increase. The second significant opportunity lies is in keeping the circles at a distance from each other. Within this area the linking lines are organised, usually as extensions of the lines within the circles. The final decision, or perhaps the first, is the size and, particularly, the proportion of the frame within which the design is to be made, and the size of the circles that are to be located within it.
A more complex pattern and its sub-grid
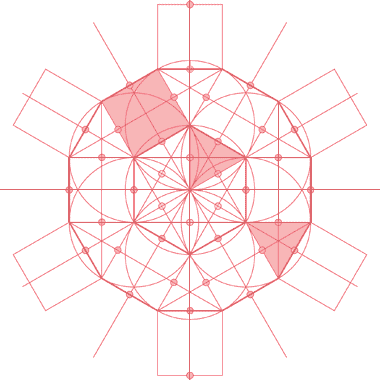
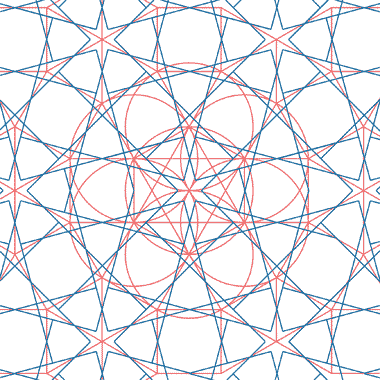
In the majority of the examples that have been illustrated on these pages, the patterns which have been developed have used grids which are formed directly from the basic lines and their intersections established by the simple geometric patterns selected – five-point, six-point and so on…
However, more sophisticated patterns can be created when increasingly complex sub-grids are developed which offer additional points of selection for the designer. The simplest way of developing a more complex design is to create a sub-grid associated with the central points of the lines of the simpler underlying geometric construction. One of the consequences of this is that the patterns created can appear to be more dynamic than those established on a less complex and more usual basis.
As an example, the design developed here has been established on the sub-divisioning of a central circle, which has a hexagon constructed on it from which a basic dodecagon is developed. On this hexagon and dodecagon, polygons are developed consisting of equilateral triangles and squares, each side having the same length as the originating hexagon. On the sides of these polygons, points are located which lie half way along them – shown here as the small circles.
The second diagram illustrates how these central points may be linked in order to establish the lines on which a pattern might be designed. The lines in red are those shown in the first diagram above, developed to extend to the outside of the diagram, the lines in blue are those which join or pass through points on the centres of the lines in red.

This third diagram shows, at a different scale, how the sub-grid appears with the basic hexagon and dodecagon removed. There are two points to note here; firstly the way in which there are implied patterns that appear and disappear as the image is scanned – and which are not always formed of continuous lines or shapes and, secondly, the patterns of squares of different sizes which run through the diagram at varying angles.

The diagram above gives a suggestion of the variety of patterns that might be constructed upon it. The grid shows a relatively even disposition of lines and spaces which allow a greater feeling of the infinite coverage common to traditional Islamic patterning. This diagram shows something of that character by illustrating the patterns stretching over a greater area. Looking at it, even at this scale, you will find your eye moving around as it recognises patterns constantly forming and reforming.

Here is the finished pattern based solely on the sub-grid divisioning of basic grid illustrated in the diagram above. What is particularly notable is the range of pentagonal shapes which, due to their irregularity, helps in the creation of a static design, yet one which has a considerable degree of mobility to it. But this mobility has much to do with the selection of shapes and the colours used.

In the pattern above, no colour has been applied to the six and eight sided shapes in order to concentrate the eye on the patterns created by the stars, but it is obvious that with development of both the lines and the shapes a wide variety of patterns can be created, dependent upon the colours, tones and selections made. In this design, shown at the same scale, a simple range of colours has changed the character of the pattern, in a sense, making it less fluid. Using more strongly contrasting colours or tones, the pattern can be changed considerably, including an apparent change of scale – though apparently decreasing fluidity with increased contrast.

Although these patterns can be thought of as extending infinitely in two directions, one of the characteristics of patterns created on a hexagonal grid is that although there is symmetry in both a vertical and horizontal direction, rotating the pattern through 90° creates a significantly different visual effect. Because the eye tends to read what is in front of it horizontally, patterns which have a strong vertical element in them tend to appear more restrictive. In that sense, the eye flows more easily over the image on the left than it does on the right in this illustration, a distinction which can be used to effect by designers when considering covering a plane surface.
A basic construction for sixteen-point patterns

This diagram has been placed here in order to show how a basic framework can be constructed which will allow those with an interest in sixteen-point patterns to make a start.
The illustration assumes that the drawing is being made with compasses and straight edge though most will use software if they are drawing digitally – an easier proposition to construct.
With one point of a pair of compasses on a horizontal line, describe a circle. With compasses set to a larger radius, draw arcs above and below the horizontal line, their centres at the two intersections of the first circle and horizontal line. Through the two arc intersections, raise a vertical line.
With the compasses set to the radius of the first circle and one point at each of the intersections of the horizontal and vertical lines with the circumference, draw arcs and join them with two lines passing through the centre at 45°.
Draw horizontal and vertical lines through the intersections of the two 45° diagonals with the circumference. This will create four squares with coincident corners at the centre of the circle and diameters the radius of the circle.
With the compasses set at the original radius and their points at the intersection of the 45° diagonals and central circumference, draw two more circles. Draw a line connecting the intersection of these circles with the diagonals. Extend lines at right angles to this line through the intersections of the last two circles with the central vertical line, and then joint the intersections of these two lines and diagonal lines to complete an outer square.
Finally, draw lines from the intersections of the external diameters of the circles through the centre of the original circle, thus establishing lines at 22.5° to the horizontals and verticals.
A sixteen point geometrical pattern


The pattern developed immediately above is just one of a number which can be constructed either to stand on its own or as an element of an infinitely repeating pattern. The pattern shown on these two graphic sketches is just one of many alternative designs and has been developed from a ceramic tiling pattern on a wall in the Alhambra, Spain. In fact there are a number of examples of this pattern applied to ceramic tiling within the Alhambra.
The pattern is based on a circle contained within a square with a side the same length as the diameter of the circle. Four circles with the same diameter as the central circle are grouped with their centres at the mid-point of the sides of the square.
The small circle in the centre has the same radius as the small quadrant circles in the corners of the square, and the eight small circles have their centres at the intersection of the central square on the diagonal with the four quadrant circles in the corners.
From that basis it is possible to draw a series of construction or guide lines enabling the pattern to evolve.
The lower illustration, an animation of the development of the design, is based on the central square above and illustrates step by step the lines necessary upon which to construct the final pattern. Unlike the illustration above, all the lines are shown the same colour as there are over thirty steps to create the complete guide layout.
The guides have been established relatively logically but there are issues with a number of decisions for which logical guides seemed impossible to find. This will have to be looked at again as it seems there must be solutions I have yet to find.

At the top of this page there are some examples of designs which were created on a variety of materials. The last of the group is a tile whose pattern has a sixteen-pointed star at its centre. It is reproduced here as the background to the sixteen-pointed star immediately above, here shown in white for contrast.
The white overlaid pattern is not intended to be a perfect fit, nor is it meant to fit the overall tile, but is placed to illustrate the common central rosette which can be seen to have the same setting out as the Moroccan tile, particularly in the width of the sixteen points of the central star. The latter is obviously larger and has a different construction for the extended pattern, this being dependent upon its relationship with adjacent tiles.

It is evident that the Moroccan tile and the second pattern have been laid out very differently so, finally, here is a very rough comparison between the two sixteen-pointed star patterns, the central star being approximately the same size in both cases, and where the surrounding pattern of the Moroccan tile can be seen to be considerably more complex than that of the simpler pattern.
An eighteen and twelve point geometrical pattern

This photograph, a detail of an old pair of doors to the Grand Mosque in Mecca, Saudi Arabia is a beautiful example of Islamic geometric design. It demonstrates perfectly the attraction of geometric adornment with what appears at first sight to be a simple application of a linear pattern selectively raised to produce three-dimensional relief. In this case the underlying geometry has been developed with considerable modeling added to enhance the door, creating a heavily modeled design that benefits from cast shadows.

In order to study the panels I have taken the liberty of amending the photograph slightly in order to make it more accurate geometrically and, therefore, easier to investigate its underlying structure, but essentially this is how it appears. The door has a similar layout to many other panels in that there is a grouping of large rosettes with smaller rosettes between them. The design structure is also similar in that the larger and smaller rosettes are both distributed to fall on the centres of a six-pointed framework, the two frameworks being set at 30° to each other.
The photograph above shows, like many of the panel patterns seen in Islamic design, only a part of a regular geometric patterning that extends, in theory, to infinity. In the illustration below it you can see how the pattern selected to enliven the door relates to this infinitely patterned ground, as well as the relationship between the underlying frameworks of the different rosettes.

Although I have had to construct the geometry of the rosettes from scratch, I have generally omitted much of the constructions from these sketches in order to keep them relatively simple. Having said that I have obviously included much that is not easily seen as I have to admit to finding the density of lines an added attraction to the studies. This sketch is such an example, the larger 18-point rosettes have been laid out with red lines, the smaller, 12-point rosettes with blue lines. The illustration shows, on the left, the setting out of the two different types of rosettes and, on the right, the basic relationships of those rosettes. The linking geometries have been omitted. The sketch shows the relationship with the pattern on the door and can be compares with the diagram above.


These next two sketches illustrate the point made relating to the incorporation of detail. This first sketch shows the basic geometry created by the two rosettes but to which I have added the linking geometry that fills the spaces between the two rosettes. Below it is a sketch showing most of the geometry used to produce the rosettes, though omitting a little of it for clarity. There are two points to make here; the first is that there is a degree of choice allowed the designer in selecting which linking geometries may best be used. Secondly, there are always complications introduced when thin construction lines are developed into wider channels as can be seen in the photograph of the doors. This introduces another series of possibilities for constructing the design. What is apparent is that there are eccentricities in the setting out of the door, but I find this part of the attraction of craftsmen’s work.


In order to clarify the design, here I have simplified the geometry again and given a degree of colour to the different elements – the two rosettes and the linking geometry. As I mentioned above, the linking geometry has a degree of selection to it which is usually resolved through linkages that produce irregular four- and five-point stars. The stars I have produced here are not as accurate as they should be, but I hope they are good enough to understand.
Below it I have placed the same photograph shown at the top of this note, but this time with the geometric pattern superimposed on it. There is a small lack of coincidence, but I think it is good enough to see how the designer took a panel design and applied it to a pair of doors. He might have elected to produce two panels, one for each door leaf, but I believe the use of a single panel, simply divided and heavily modeled, has produced a powerful design, and one well suited to introducing those who came to worship at the Grand Mosque.
A twelve, six and seven point geometrical pattern

This first illustration is a continuous pattern developed from one I came across and thought attractive, hoping to be able to analyse and construct it readily, particularly because the pattern incorporates a seven-pointed element in its design. However, this illustration is only an approximation of the geometrical pattern I saw.
Realising that the seven-point shape within it is difficult to construct accurately, I particularly wanted to investigate its relationship with the two other main design elements contained within the pattern – the twelve- and six-sided shapes. This design is placed here to illustrate an inability to come to an understanding of what should be an accurate and logically developed construction, with the hope that the design might be re-examined and resolved to my own satisfaction at some time in the future.

Regrettably I have been unable to create a pattern as I had hoped, one based on logical connections between the main geometries. The version of the pattern illustrated in these first two graphics relies on adopting a seven-point geometry in the form of an irregular, though symmetrical, heptagon. I had hoped to be able to construct a regular – or an approximation of a regular one – in its place.
The second of these illustrations shows a reduction of the first pattern into a rosette of seven connected twelve-point stars or shapes with, bottom right, the seven elements which make up the overall pattern. The irregular heptagons can be seen to be the shapes which surround each of the twelve-pointed stars. It can also be seen that there are six groups of three irregular heptagons each surrounding a smaller regular hexagon, themselves surrounding the central twelve-pointed star.
These next two illustrations are reductions of background workings made in the production of the pattern shown above. They are placed here as they show something of the working out of the patterns shown here. Much of the construction of the pattern is not shown in these graphics – mainly the constructions required to divide the circles into twelve parts, the construction of the square between them and some of the tentative exploratory lines used to determine the smaller elements of the pattern – but the lines remaining here demonstrate the setting out of the central part of the design, the establishing of two of the twelve-pointed stars and two possible arrangements for the hexagons and irregular heptagons located between them.
Bear in mind that, for a degree of clarity, these two larger graphics are shown with the central square having its sides established horizontally and vertically, whereas the coloured pattern shown above them is based on the whole of this construction being rotated clockwise by 15°.
As mentioned above, the pattern has a construction slightly different from the two constructions shown here. The differences can be seen in the sizing of the hexagons and heptagons, the hexagon being larger and the heptagon, particularly, being noticably different in the lengths of its sides.

The last of these graphics compares a detail of the two workings shown above, concentrating on the hexagons and heptagons established between the two dodecagons. The detail on the left attempted to create the heptagon first on the basis of a circle drawn tangent to both circles containing the dodecagons. The detail on the right set out the hexagon first, and then made an attempt to create the heptagon. Neither of them creates a more or less regular heptagon.
More work needs to be carried out in order to create a more regular sided heptagon, but I suspect this will only be possible by inspection and guesswork. What is evident, is that it is imperative to determine accurately the spacing between the two dodecagons.
A Moroccan pattern

Geometric patterns which are similar to each other can be seen all over the Islamic world, and elsewhwere, of course. But those we associate with the Islamic world exhibit many similarities, in some regard due to the materials used but also for their use of the same geometries, but with many local variations and colour selections.
This particular pattern can be seen all over Morocco but is shown here where it is used in one of the external panels of the Hassan II masjid in Casablanca, Morocco where its strong form frames small recessed panels of mosaic designs which do not have the character of geometry found in much of the Islamic world but appear to be almost illustrative in appearance.

However, it is the construction of the frame design which is of interest in these pages, and this example is unusual in that it appears to be based on semi-circles broken in their centre and moved apart horizontally. Examination of the design shows that there are a number of variations which can be constructed where the proportions vary, but the purpose here is to record a single geometric construction from which variations might be assumed. In this case it can be seen that the individual frame is wider than the example which was photographed on the Hassan II masjid, and has been set out starting with a simple pair of rectangles having the same size, but one of them being rotated at 90° to the other. In the following diagams, not all of the construction lines have been shown in order to simplify the explanation.

Start by constructing a rectangle with the sides in the proportion 3:2. This can be effected by constructing two squares adjacent to each other, and halving one of them. Copy this, rotate it 90° and place it symmetrically on top of the first rectangle.
With the top corners of the vertical rectangle as their centres, describe two circles each with a radius of the shorter side of the rectangle. Repeat this by drawing two more circles of the same radius with their centres at the bottom corners of the horizontal rectangle.
Identify four quadrants of the four circles which intersect; when intersected, these will form part of the sides of the basic pattern unit. Join the quadrants by lines which intersect with the corners of the intersected two rectangles. This will create the basic pattern which can be repeated infinitely.
Note that the pattern constructed above is different from that shown in the photograph over it where the basic design appears to be narrower in width. One of the clues to this is that the design outlined here is established at an angle of 45° from the vertical, whereas the design photographed in Casablanca measures around 38° from the vertical. Inspection of the Casablanca design shows that while the foot of the arcs start at 90° from a horizontal line, the top of the arc doesn’t reach a tangent to a horizontal line at its high point – nor does it appear to be a segment of a complete semi-circle.

On the left of this diagram is the tile constructed above and, on the right is a tile constructed on the basis of the contained rectangle being different from the 3:2 of the original tile. That on the right has the proportions 5:2 and the repeat pattern sits at around 37°. Although this seems more similar to the original design, it can be seen from inspection, particularly at the lowest part of the geometry, that it is still not an accurate reconstruction of the original Moroccan pattern – but that there are squares contained within both patterns, shown in a thin blue line. More work is needed…
A Moroccan pattern based on the Golden Section

Following a study of a Moroccan pattern, immediately above and repeated here on the right, what follows is believed to be a generic geometric construction of that specific pattern. Note the subtle differences between that constructed based on the Golden section – below – and the pair immediately above.
Note that the photograph of the pattern shows it to be narrower than that which is set out here and is unlikely to have been established from the Golden Section, but from a variation.
Essentially, the design set out here is established on the geometry of the Golden Section with the setting out developing from a rectangle with the sides in the ratio of approximately 1:1.618, the internal angle of the Golden Section being 58·28° – or 58.282525588538995° for the record.

Begin by constructing a square on a horizontal line. In order to construct a rectangle with the proportions of the Golden Section, halve the square vertically and, from the intersection of the halving line with the bottom of the square, describe an arc with its radius the line between the intersection of the base of the square and its top corner.
A rectangle in the ratio of the Golden Section will be formed from this junction to the top right corner of the square.
Draw a vertical line through the centre of the rectangle and construct three more rectangles of the same Golden Section proportion and size, turning each through 90° and placing two coincident with the vertical sides of the original rectangle and with the same base, and the third centred below it, again with its top coincident with the horizontal line.
With their centres at the top corners of the lowest rectangle, and their radius set to the outside lower corner of the upper rectangles, draw two circles. With the same radius, draw two more circles with their centres at the inner top corners of the two upper rectangles.
In order to establish the squared elements of the eventual tile pattern, draw vertical lines tangential to the outsides of the last two circles, extend vertical lines from the inner sides of the two upper rectangles, and extend horizontal lines along the bottom of the lower rectangle and the top of the upper rectangles.
From the intersections of the lowest horizontal line with the inner two vertical lines draw two more circles with the same diameters as the previous four. From the intersections of the outer two vertical lines with the initial horizontal line, draw the final two circles, again with the same diameter as the previous six.
All the necessary lines required to establish the outline of the design are now in place and can be used selectively to intersect and create the basic design based on the Golden Section.

An illustrated note describing an accurate construction of this pattern has been set out immediately above, but the intention of this graphic is to demonstrate the relatively simple geometric rhythm which lies behind this pattern, commonly associated with Morocco.
Only two shapes are required to establish the pattern: a square and a rectangle, the latter having its proportions based on the Golden Section, and with its longer side having the same length as the sides of the square. The grid is simple; it has the two shapes repeating alternately horizontally, each row being established with the rectangle centred on a square above and below.
It is possible, if not probable, that with a simple template of the Golden Section rectangle, this might be the basis on which artisans fabricated, and continue to fabricate the design.
more to be written…
Arabic / Islamic design | top | Arabic / Islamic geometry 02
Search the Islamic design study pages
- Introduction
- Arabic / Islamic design
- Arabic / Islamic geometry 01
- Arabic / Islamic geometry 02
- Arabic / Islamic geometry 03
- Arabic / Islamic geometry 04
- Islamic architecture
- Islamic urban design 01
- Islamic urban design 02
- Islamic urban design 03
- Islamic urban design 04
- Islamic urban design 05
- Arabic / Islamic gardens
- Gulf architecture 01
- Gulf architecture 02
- Gulf architecture 03
- Gulf architecture 04
- Gulf architecture 05
- Gulf architecture 06
- Gulf architecture 07
- Gulf architecture 08
- Infrastructure development
- The building industry
- Environmental control
- Perception
- The household on its lot
- A new approach – conceptual
- A new approach – principles
- A new approach – details
- Al Salata al jadida
- Public housing
- Expatriate housing study
- Apartment housing
- Pressures for change
- The State’s administration
- Society 01
- Society 02
- Society 03
- Society 04
- Society 05
- Society 06
- History of the peninsula
- Geography
- Planning 01
- Planning 02
- Population
- Traditional boats
- Boat types
- Old Qatar 01
- Old Qatar 02
- Security
- Protection
- Design brief
- Design elements
- Building regulations
- Glossary
- Glossary addendum
- References
- References addendum
- Links to other sites